
【题目】已知正方形![]() 在平面直角坐标系中,点
在平面直角坐标系中,点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上,等腰直角三角形
轴的正半轴上,等腰直角三角形![]() 的直角顶点
的直角顶点![]() 在原点,
在原点,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,
,![]() .将
.将![]() 绕点
绕点![]() 逆时针旋转,得
逆时针旋转,得![]() 点
点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .
.
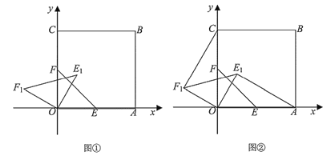
(Ⅰ)①如图①,求![]() 的长;②如图②,连接
的长;②如图②,连接![]() ,
,![]() ,求证
,求证![]() ;
;
(Ⅱ)将![]() 绕点
绕点![]() 逆时针旋转一周,当
逆时针旋转一周,当![]() 时,求点
时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
【答案】(Ⅰ)①![]() ;②见解析;(Ⅱ)点
;②见解析;(Ⅱ)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)①根据勾股定理求出EF的长,![]() 的长;根据SAS定理证明
的长;根据SAS定理证明![]() 即可;
即可;
(2)由于△OEF是等腰Rt△,若OE∥CF,那么CF必与OF垂直;在旋转过程中,E、F的轨迹是以O为圆心,OE(或OF)长为半径的圆,若CF⊥OF,那么CF必为⊙O的切线,且切点为F;可过C作⊙O的切线,那么这两个切点都符合F点的要求,因此对应的E点也有两个;在Rt△OFC中,OF=2,OC=OA=4,可证得∠FCO=30°,即∠EOC=30°,已知了OE的长,通过解直角三角形,不难得到E点的坐标,由此得解.
解:(Ⅰ)①∵等腰直角三角形![]() 的直角顶点
的直角顶点![]() 在原点,
在原点,![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() .
.
∵![]() 是由
是由![]() 绕点
绕点![]() 逆时针旋转得到的,
逆时针旋转得到的,
∴![]() .
.
②∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,
∵将![]() 绕点
绕点![]() 逆时针旋转,得
逆时针旋转,得![]() ,
,
∴![]() ,
,
又![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() .
.
(Ⅱ)如图,
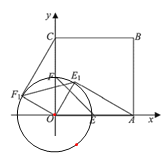
∵OE⊥OF,
∴过点F与OE平行的直线有且只有一条,并与OF垂直,
当三角板OEF绕O点逆时针旋转一周时,
则点F在以O为圆心,以OF为半径的圆上.
∴过点F与OF垂直的直线必是圆O的切线.
又点C是圆O外一点,过点C与圆O相切的直线有且只有2条,不妨设为CF1和CF2,
此时,E点分别在E1点和E2点,满足CF1∥OE1,CF2∥OE2.
当切点F1在第二象限时,点E1在第一象限.
cos∠COF1=![]() ,
,
∴∠COF1=60°,∴∠AOE1=60°.
∴点E1的横坐标为:xE1=2cos60°=1,
点E1的纵坐标为:yE1=2sin60°=![]() ,
,
∴点E1的坐标为(1,![]() );
);
当切点F2在第一象限时,点E2在第四象限.
同理可求:点E2的坐标为(1,-![]() ).
).
综上所述,三角板OEF绕O点逆时针旋转一周,存在两个位置,使得OE∥CF,
此时点E的坐标为E1(1,![]() )或E2(1,-
)或E2(1,-![]() ).
).


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】数学课上,老师提出了这样一个问题:如图,己知![]() .求作:过
.求作:过![]() 三点的圆.
三点的圆.
小芸是这样思考的:圆心确定一个圈的位置,半径确定一个圆的大小要作同时经过几个定点的圆,就是要先找到一个点,使得这个点到这几个定点的距离都相等.这样既定了圆心,又定了半径,就能画出满足条件的圆了.
小智听了小芸的分析后,按照这个思路很快就画出了一个过![]() 三点的圆.
三点的圆.
请你在答题纸上而出这个圆,并写出作图的主要依据,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4的网格中,每一个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,以O为坐标原点建立如图所示的平面直角坐标系.若抛物线y=x2+bx+c的图象至少经过图中(4×4的网格中)的三个格点,并且至少一个格点在x轴上,则符合要求的抛物线一定不经过的格点坐标为( )
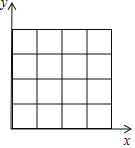
A.(1,3)B.(2,3)C.(1,4)D.(2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 上,同时,抛物线
上,同时,抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 上,那么我们称抛物线
上,那么我们称抛物线![]() 与
与![]() 关联.
关联.
(1)已知抛物线![]() :
:![]() 与
与![]() :
:![]() ,请判断抛物线
,请判断抛物线![]() 与抛物线
与抛物线![]() 是否关联,并说明理由.
是否关联,并说明理由.
(2)抛物线![]()
![]() ,动点
,动点![]() 的坐标为
的坐标为![]() ,将抛物线绕点
,将抛物线绕点![]() 旋转180°得到抛物线
旋转180°得到抛物线![]() ,若抛物线
,若抛物线![]() 与
与![]() 关联,求抛物线
关联,求抛物线![]() 的解析式.
的解析式.
(3)点![]() 为抛物线
为抛物线![]() :
:![]() 的顶点,点
的顶点,点![]() 为抛物线
为抛物线![]() 关联的抛物线的顶点,是否存在以
关联的抛物线的顶点,是否存在以![]() 为斜边的等腰直角三角形ABC,使其直角顶点
为斜边的等腰直角三角形ABC,使其直角顶点![]() 在直线
在直线![]() 上?若存在,求出
上?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
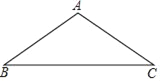
【题目】如图,在△ABC中,AB=AC=5,sinC=![]() ,将△ABC绕点A逆时针旋转得到△ADE,点B、C分别与点D、E对应,AD与边BC交于点F.如果AE∥BC,那么BF的长是____.
,将△ABC绕点A逆时针旋转得到△ADE,点B、C分别与点D、E对应,AD与边BC交于点F.如果AE∥BC,那么BF的长是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,四边形ABCD内接于以BC为直径的圆,圆心为O,且AB=AD,延长CB、DA交于P,过C点作PD的垂线交PD的延长线于E,且PB=BO,连接OA.
(1)求证:OA∥CD;
(2)求线段BC:DC的值;
(3)若CD=18,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]() :
:![]() (
(![]() 、
、![]() 、
、![]() 为常数,且
为常数,且![]() )与
)与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线![]() 的表达式;
的表达式;
(2)将![]() 平移后得到抛物线
平移后得到抛物线![]() ,点
,点![]() 、
、![]() 在
在![]() 上(点
上(点![]() 在点
在点![]() 的上方),若以点
的上方),若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是正方形,求抛物线
为顶点的四边形是正方形,求抛物线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com