
【题目】如图所示,已知抛物线y=﹣x2+bx+c与x轴相交于A、B两点,且点A的坐标为(1,0),与y轴交于点C,对称轴直线x=2与x轴相交于点D,点P是抛物线对称轴上的一个动点,以每秒1个单位长度的速度从抛物线的顶点E向下运动,设点P运动的时间为t(s).
(1)点B的坐标为 ,抛物线的解析式是 ;
(2)求当t为何值时,△PAC的周长最小?
(3)当t为何值时,△PAC是以AC为腰的等腰三角形?

【答案】(1)(3,0),y=﹣x2+4x﹣3;(2)t=2;(3)t=4或4+![]() 或4﹣
或4﹣![]() .
.
【解析】
(1)把A点坐标与对称轴x=1代入解析式即可求出b,c的值,即可求出解析式,故求出B点坐标;(2)由图可知,AC是定长,故只要求出PA+PC最小时,则△PAC的周长最小,又点A关于对称轴x=2的对称点是点B,故连接BC与抛物线对称轴的交点即为P点,此时PA+PC最小,则求出直线BC的解析式与x=2的交点即为P点坐标继而求出t的值;(3)根据AC为腰可分两种情况,①CP=AC,可作图,根据AC=CP=![]() ,CF=2,利用勾股定理可求出PF的长,继而求出时间t,注意还要要分两种情况,②AC=AP,可作图,利用Rt△OAC≌Rt△DAP,得出DP=CO=3,故而求出EP的长,即可求出时间t.
,CF=2,利用勾股定理可求出PF的长,继而求出时间t,注意还要要分两种情况,②AC=AP,可作图,利用Rt△OAC≌Rt△DAP,得出DP=CO=3,故而求出EP的长,即可求出时间t.
解:(1)根据题意得: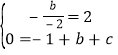
解得:b=4,c=﹣3
∴抛物线解析式y=﹣x2+4x﹣3
当y=0时,0=﹣x2+4x﹣3
∴x1=1,x2=3
∴点B(3,0)
故答案为:(3,0),y=﹣x2+4x﹣3
(2)如图:
∵△PAC的周长=AC+PA+PC
且AC是定长,
∴PA+PC最小时,△PAC的周长最小
∵点A,点B关于对称轴直线x=2对称
∴连接BC交对称轴直线x=2于点P
∵y=﹣x2+4x﹣3与y轴交于点C,点E为抛物线的顶点
∴点C(0,﹣3),点E(2,1)
∴OC=3,点D(2,0)即DE=1
∵点B(3,0),点C(0,﹣3)
∴直线BC解析式:y=x﹣3
当x=2时,y=﹣1
∴点P(2,﹣1)
∴t=![]() =2
=2
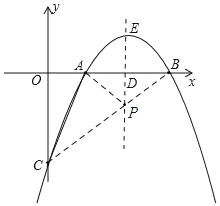
(3)若CP=AC时,如图:过点C作CF⊥ED于点F
∵点A(1,0),点C(0,﹣3)
∴OA=1,OC=3
∵AC=![]() =
=![]()
∵CF⊥DE,DE⊥OD,OC⊥OD
∴四边形ODFC是矩形
∴CF=OD=2,DF=OC=3
∵AC=CP=![]() ,CF=2
,CF=2
∴PF=![]() =
=![]()
∴DP=3±![]()
∴EP=4±![]()
∴t1=![]() =4+
=4+![]() ,t2=
,t2=![]() =4﹣
=4﹣![]()
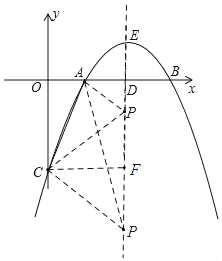
若点AC=AP时,如图
∵点A(1,0),点D(2,0)
∴OA=AD=1,且AC=AP
∴Rt△OAC≌Rt△DAP(HL)
∴OC=DP=3
∴EP=4
∴t=![]() =4
=4
综上所述:t=4或4+![]() 或4﹣
或4﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
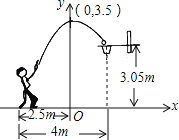
A. 此抛物线的解析式是y=﹣![]() x2+3.5
x2+3.5
B. 篮圈中心的坐标是(4,3.05)
C. 此抛物线的顶点坐标是(3.5,0)
D. 篮球出手时离地面的高度是2m
查看答案和解析>>
科目:初中数学 来源: 题型:
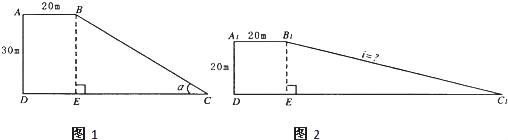
【题目】一段路基的横断面是直角梯形,如图1,已知原来坡面的坡角α的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如右下图2的技术要求.试求出改造后坡面的坡度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc>0;②a﹣b+c<0;③2a+b>0;④b2﹣4ac>0;正确的有( )个.
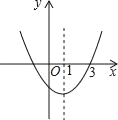
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
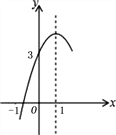
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
① 4ac<b2;② 方程ax2+bx+c=0的两个根是![]() ;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
其中结论正确有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F,则下列选项中的结论错误的是( )
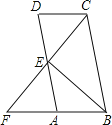
A. FA:FB=1:2 B. AE:BC=1:2
C. BE:CF=1:2 D. S△ABE:S△FBC=1:4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的书包里只放了A4大小的试卷共4张,其中语文2张、数学1张、英语1张.
![]() 若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率为______;
若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率为______;
![]() 若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______.
若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③![]() ,④OD:OC=DE:EC,⑤
,④OD:OC=DE:EC,⑤![]() ,正确的有( )
,正确的有( )
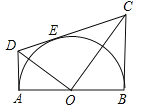
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com