
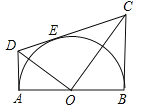
【题目】如图,AB为半圆O的在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③![]() ,④OD:OC=DE:EC,⑤
,④OD:OC=DE:EC,⑤![]() ,正确的有( )
,正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
【答案】D
【解析】
试题连接OE,如图所示:∵AD与圆O相切,DC与圆O相切,BC与圆O相切,∴∠DAO=∠DEO=∠OBC=90°,∴DA=DE,CE=CB,AD∥BC,∴CD=DE+EC=AD+BC,选项②正确;
在Rt△ADO和Rt△EDO中,∵OD=OD,DA=DE,∴Rt△ADO≌Rt△EDO(HL),∴∠AOD=∠EOD,同理Rt△CEO≌Rt△CBO,∴∠EOC=∠BOC,又∠AOD+∠DOE+∠EOC+∠COB=180°,∴2(∠DOE+∠EOC)=180°,即∠DOC=90°,选项①正确;
∴∠DOC=∠DEO=90°,又∠EDO=∠ODC,∴△EDO∽△ODC,∴![]() ,即
,即![]() ,选项⑤正确;
,选项⑤正确;
∵∠AOD+∠COB=∠AOD+∠ADO=90°,∠A=∠B=90°,∴△AOD∽△BOC,∴![]() ,选项③正确;
,选项③正确;
同理△ODE∽△OEC,∴![]() ,选项④正确;
,选项④正确;
故选D.



科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=﹣x2+bx+c与x轴相交于A、B两点,且点A的坐标为(1,0),与y轴交于点C,对称轴直线x=2与x轴相交于点D,点P是抛物线对称轴上的一个动点,以每秒1个单位长度的速度从抛物线的顶点E向下运动,设点P运动的时间为t(s).
(1)点B的坐标为 ,抛物线的解析式是 ;
(2)求当t为何值时,△PAC的周长最小?
(3)当t为何值时,△PAC是以AC为腰的等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
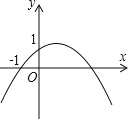
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是
A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B,与
与x轴交于点A,B,与![]() 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。

(1)求该抛物线的解析式;
(2)求梯形COBD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】炮弹的运行轨道若不计空气阻力是一条抛物线.现测得我军炮位A与射击目标B的水平距离为600m,炮弹运行的最大高度为1200m.
(1)求此抛物线的解析式;
(2)若在A、B之间距离A点500m处有一高350m的障碍物,计算炮弹能否越过障碍物.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,将两个全等的等腰直角![]() 和
和![]() 摆放在一起,
摆放在一起,![]() 为公共顶点,
为公共顶点,![]() ,它们的斜边长为2,若
,它们的斜边长为2,若![]() 固定不动,
固定不动,![]() 绕点
绕点![]() 旋转,
旋转,![]() 、
、![]() 与边
与边![]() 的交点分别为
的交点分别为![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合,点
重合,点![]() 不与点
不与点![]() 重合),设
重合),设![]() ,
,![]() .
.

(1)请在图中找出两对相似而不全等的三角形,并选取其中一对加以证明.
(2)求![]() 与
与![]() 的函数关系式,直接写出自变量
的函数关系式,直接写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
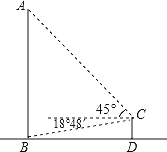
【题目】全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为 米(参考数据:tan78°12′≈4.8).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com