
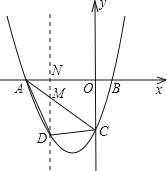
【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,
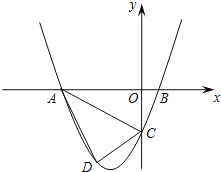
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
【答案】(1)![]() ;(2)四边形ABCD面积有最大值
;(2)四边形ABCD面积有最大值![]() .
.
【解析】
(1)已知B点坐标,易求得OB、OC的长,进而可将B、C的坐标代入抛物线中,求出待定系数的值,即可得出抛物线的解析式.
(2)根据A、C的坐标,易求得直线AC的解析式.由于AB、OC都是定值,则△ABC的面积不变,若四边形ABCD面积最大,则△ADC的面积最大;可过D作x轴的垂线,交AC于M,x轴于N;易得△ADC的面积是DM与OA积的一半,可设出N点的坐标,分别代入直线AC和抛物线的解析式中,即可求出DM的长,进而可得出四边形ABCD的面积与N点横坐标间的函数关系式,根据所得函数的性质即可求出四边形ABCD的最大面积.
(1)∵B(1,0),
∴OB=1;
∵OC=3BO,
∴C(0,﹣3);
∵y=ax2+3ax+c过B(1,0)、C(0,﹣3),
∴![]() ;
;
解这个方程组,得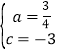 ,
,
∴抛物线的解析式为:y=![]() x2+
x2+![]() x﹣3;
x﹣3;
(2)过点D作DM∥y轴分别交线段AC和x轴于点M、N
在y=![]() x2+
x2+![]() x﹣3中,令y=0,
x﹣3中,令y=0,
得方程![]() x2+
x2+![]() x﹣3=0解这个方程,得x1=﹣4,x2=1
x﹣3=0解这个方程,得x1=﹣4,x2=1
∴A(﹣4,0)
设直线AC的解析式为y=kx+b
∴![]() ,
,
解这个方程组,得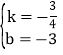 ,
,
∴AC的解析式为:y=﹣![]() x﹣3,
x﹣3,
∵S四边形ABCD=S△ABC+S△ADC
=![]() +
+![]() DM(AN+ON)
DM(AN+ON)
=![]() +2DM
+2DM
设D(x,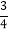 x2+
x2+![]() x﹣3),M(x,﹣
x﹣3),M(x,﹣![]() x﹣3),
x﹣3),
DM=﹣![]() x﹣3﹣(
x﹣3﹣(![]() x2+
x2+![]() x﹣3)=﹣
x﹣3)=﹣![]() (x+2)2+3,
(x+2)2+3,
当x=﹣2时,DM有最大值3
此时四边形ABCD面积有最大值=![]() +2×3=
+2×3=![]() .
.


科目:初中数学 来源: 题型:
【题目】某校初三有2000名学生,为了解初三学生的体能,从人数相等的甲、乙两个班进行了抽样调查,过程如下,请补充完整.
收集数据:从甲、乙两个班各随机抽取20名学生.进行了体能测试,测试成绩(百分制)如下:
甲:78,86,74,81,75,76,87,70,75,90,75,79, 81,70, 74, 80 ,86, 69 ,83, 77.
乙:93,73,88,81,72,81,94,83,77,83,80,81,70,81,73,78,82,80,70,40.
整理、描述数据:按如下分数段整理、描述这两组样本数据:
成绩 |
|
|
|
|
|
|
甲班 | 0 | 0 | 1 | 11 | 7 | 1 |
乙班 | 1 | 0 | 0 | 7 | 10 | 2 |
(说明:成绩80分及以上为体能优秀,70~79分为体能良好,60~69分为体能合格,60分以下为体能不合格)
分析数据:两组样本数据的平均数、中位数、众数如下表所示:
班级 | 平均数 | 中位数 | 众数 | 优秀率 |
甲 | 78.3 | 77.5 | b | 40% |
乙 | 78 | a | 81 | c |
问题解决:
(1)表中a= ,b= ,c ;
(2)估计一下该校初三体能优秀的人数有多少人?
(3)通过以上数据的分析,你认为哪个班的学生的体能水平更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠BAO=30°,AB=BO,反比例函数y=![]() (x<0)的图象经过点A
(x<0)的图象经过点A
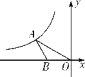
(1)求∠AOB的度数
(2)若OA=![]() ,求点A的坐标
,求点A的坐标
(3)若S△ABO=![]() ,求反比例函数的解析式
,求反比例函数的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
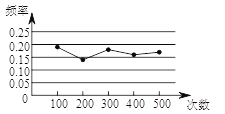
A. 袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球
B. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
C. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() (
(![]() )的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;
②3a+b<0;
③![]() ;
;
④![]() ;
;
其中正确的结论是( )
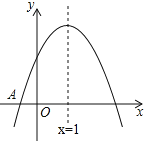
A.①③④B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
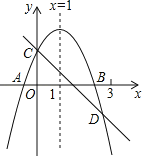
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC:BC:AB=5:12:13,⊙O在△ABC内自由移动,若⊙O的半径为1,且圆心O在△ABC内所能到达的区域的面积为![]() ,则△ABC的周长为_____.
,则△ABC的周长为_____.
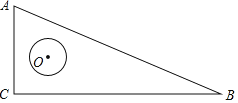
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为
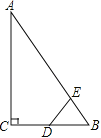
A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 定义:在凸四边形中,我们把两组对边乘积的和等于对角线的乘积的四边形称为“完美四边形”
(1)在正方形、矩形、菱形中,一定是“完美四边形”的是______.
(2)如图1,在△ABC中,AB=2,BC=![]() ,AC=3,D为平面内一点,以A、B、C、D四点为顶点构成的四边形为“完美四边形”,若DA,DC的长是关于x的一元二次方程x2-(m+3)x+
,AC=3,D为平面内一点,以A、B、C、D四点为顶点构成的四边形为“完美四边形”,若DA,DC的长是关于x的一元二次方程x2-(m+3)x+![]() (5m2-2m+13)=0(其中m为常数)的两个根,求线段BD的长度.
(5m2-2m+13)=0(其中m为常数)的两个根,求线段BD的长度.
(3)如图2,在“完美四边形”EFGH中,∠F=90°,EF=6,FG=8,求“完美四边形”EFGH面积的最大值.
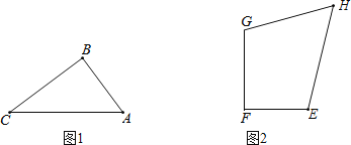
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com