
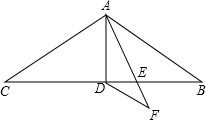
 如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( )
如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( )| A. | 4.5 | B. | 5 | C. | 5.5 | D. | 6 |
分析 根据等腰三角形三线合一的性质可得到AD⊥BC,∠BAD=∠CAD,从而可得到∠BAD=60°,∠ADB=90°,再根据角平分线的性质即可得到∠DAE=∠EAB=30°,从而可推出AD=DF,根据直角三角形30度角的性质即可求得AD的长,即得到了DF的长.
解答 解:∵△ABC是等腰三角形,D为底边的中点,
∴AD⊥BC,∠BAD=∠CAD,
∵∠BAC=120°,
∴∠BAD=60°,∠ADB=90°,
∵AE是∠BAD的角平分线,
∴∠DAE=∠EAB=30°.
∵DF∥AB,
∴∠F=∠BAE=30°.
∴∠DAF=∠F=30°,
∴AD=DF.
∵AB=11,∠B=30°,
∴AD=5.5,
∴DF=5.5
故选C.
点评 本题考查了含30°角的直角三角形,等腰三角形的判定与性质,平行线的性质等知识点,能求出AD=DF是解此题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
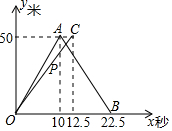 甲、乙两人在相邻两条直跑道上进行竞走比赛(注:跑道长50米,两人均往返一次,返回时转身的时间忽略不计),图中的折线OA-AB是甲离出发点的距离y(米)与比赛时间x(秒)的函数图象;线段OC是乙离出发点的距离y(米)与比赛时间x(秒)的函数图象,其中x≥0,线段OC与AB相交于点P.根据图象,解决下列问题:
甲、乙两人在相邻两条直跑道上进行竞走比赛(注:跑道长50米,两人均往返一次,返回时转身的时间忽略不计),图中的折线OA-AB是甲离出发点的距离y(米)与比赛时间x(秒)的函数图象;线段OC是乙离出发点的距离y(米)与比赛时间x(秒)的函数图象,其中x≥0,线段OC与AB相交于点P.根据图象,解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
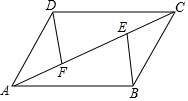 如图,E,F是四边形ABCD的对角线AC上点,AF=CE,DF=BE,DF∥BE.
如图,E,F是四边形ABCD的对角线AC上点,AF=CE,DF=BE,DF∥BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com