
ЁОЬтФПЁПШчЭМЃЌМКжЊRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃН8ЃЌBCЃН6ЃЌЕуPвдУПУы1ИіЕЅЮЛЕФЫйЖШДгAЯђCдЫЖЏЃЌЭЌЪБЕуQвдУПУы2ИіЕЅЮЛЕФЫйЖШДгAЁњBЁњCЗНЯђдЫЖЏЃЌЫќУЧЕНCЕуКѓЖМЭЃжЙдЫЖЏЃЌЩшЕуPЃЌQдЫЖЏЕФЪБМфЮЊtУыЃЎ
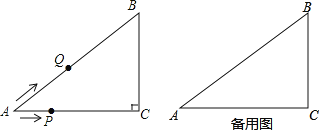
ЃЈ1ЃЉЕБtЃН2.5ЪБЃЌPQЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉОЙ§tУыЕФдЫЖЏЃЌЧѓЁїABCБЛжБЯпPQЩЈЙ§ЕФУцЛ§SгыЪБМфtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉPЃЌQСНЕудкдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкЪБМфtЃЌЪЙЕУЁїPQCЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ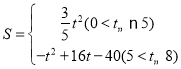 ЃЈ3ЃЉДцдкЃЎЕБtЃН
ЃЈ3ЃЉДцдкЃЎЕБtЃН![]() ЃЌtЃН
ЃЌtЃН![]() ЃЌtЃН3.4ЪБЃЌЁїPQCЮЊЕШбќШ§НЧаЮЃЎ
ЃЌtЃН3.4ЪБЃЌЁїPQCЮЊЕШбќШ§НЧаЮЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1ЃЌЙ§QзїQEЁЭACгкEЃЌСЌНгPQЃЌЧѓГіQEЃЌPEЃЌРћгУЙДЙЩЖЈРэМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉгЩШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЧѓЕУЃЛ
ЃЈ3ЃЉДцдкЃЌШчЭМ2ЃЌСЌНгCQЃЌPQЃЌЗжШ§жжЧщПіЂйЕБCQ=CPЪБЃЌЂкЕБPQ=CQЪБЃЌЂлЕБPQ=PCЪБЃЌСаЗНГЬЧѓНтМДПЩЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЙ§QзїQEЁЭACгкEЃЌСЌНгPQЃЌ
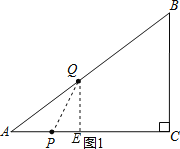
дкRtЁїABCжаЃЌЁпЁЯCЃН90ЁуЃЌACЃН8ЃЌBCЃН6ЃЌ
ЁрABЃН![]() ЃН10ЃЌ
ЃН10ЃЌ
ЁпtЃН2.5ЃЌ
ЁрAQЃН5ЃЌAPЃН2.5ЃЌ
ЁрQEЁЮBCЃЌ
![]() ,
,
![]() ,
,
ЁрQEЃН3ЃЌAEЃН4ЃЌ
ЁрPEЃН4Љ2.5ЃН1.5ЃЌ
ЁрPQЃН![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШчЭМ1ЃЌЁїABCБЛжБЯпPQЩЈЙ§ЕФУцЛ§ЃНSЁїAQPЃЌ
ЕБQдкABБпЩЯЪБЃЌSЃН![]() ЃЌЃЈ0ЃМtЁм5ЃЉ
ЃЌЃЈ0ЃМtЁм5ЃЉ
ЕБQдкBCБпЩЯЪБЃЌЁїABCБЛжБЯпPQЩЈЙ§ЕФУцЛ§ЃНSЫФБпаЮABQPЃЌ
ЁрSЫФБпаЮABQPЃНSЁїABCЉSЁїPQCЃН![]() ЁС8ЁС6Љ
ЁС8ЁС6Љ![]() ЃЈ8ЉtЃЉЃЈ16Љ2tЃЉЃНЉt2+16tЉ40ЃЌЃЈ5ЃМtЁм8ЃЉЃЛ
ЃЈ8ЉtЃЉЃЈ16Љ2tЃЉЃНЉt2+16tЉ40ЃЌЃЈ5ЃМtЁм8ЃЉЃЛ
ЁрОЙ§tУыЕФдЫЖЏЃЌЁїABCБЛжБЯпPQЩЈЙ§ЕФУцЛ§SгыЪБМфtЕФКЏЪ§ЙиЯЕЪНЪЧЃК
SЃН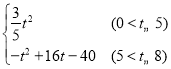 ЃЎ
ЃЎ
ЃЈ3ЃЉДцдкЃЎ
ЕБЕуQдкABБпЩЯЪБЃЌШчЭМ2ЃЌСЌНгCQЃЌPQЃЌ
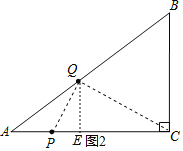
гЩЃЈ1ЃЉжЊQEЃН![]() tЃЌCEЃНACЉAEЃН8Љ
tЃЌCEЃНACЉAEЃН8Љ![]() tЃЌPQЃН
tЃЌPQЃН![]() tЃЌ
tЃЌ
ЁрCQЃН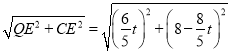 ЃЌ
ЃЌ
ЂйЕБCQЃНCPЪБЃЌ
МДЃК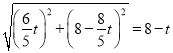 ЃЌ
ЃЌ
НтЕУЃЛtЃН![]() ЃЌ
ЃЌ
ЂкЕБPQЃНCQЪБЃЌ
МДЃК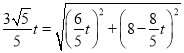 ЃЌ
ЃЌ
НтЕУЃКtЃН![]() Лђ8ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌ
Лђ8ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌ
ЂлЕБPQЃНPCЪБЃЌ
МДЃК![]() tЃН8ЉtЃЌ
tЃН8ЉtЃЌ
НтЕУЃКtЁж3.4ЃЛ
ЕБЕуQдкBCБпЩЯЪБЃЌ
ЁпЁЯACBЃН90ЁуЃЌ
ЁрЁїPQCЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрCQЃНCPЃЌ
Ёр8ЉtЃН16Љ2tЃЌ
ЁрtЃН8ЃЌЁрPЃЌQЃЌCжиКЯЃЌВЛКЯЬтвтЃЌ
злЩЯЫљЪіЃКЕБtЃН![]() ЃЌtЃН
ЃЌtЃН![]() ЃЌtЃН3.4ЪБЃЌЁїPQCЮЊЕШбќШ§НЧаЮЃЎ
ЃЌtЃН3.4ЪБЃЌЁїPQCЮЊЕШбќШ§НЧаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌCЪЧАыдВOЩЯвЛИіЖЏЕуЃЌABЮЊАыдВЕФжБОЖЃЌDЪЧЛЁBCЕФжаЕуЃЌЙ§ЕуDзїАыдВOЕФЧаЯпDEНЛACЕФбгГЄЯпгкЕуEЃЎ
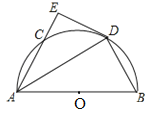
ЃЈ1ЃЉЧѓжЄЃКAEЁЭDEЃЛ
ЃЈ2ЃЉЂйвбжЊCE=2ЃЌDE=4ЃЌдђAB=ЁЁ ЁЁЃЛ
ЂкСЌНгOCЃЌDCЃЌЕБЁЯBAC=ЁЁ ЁЁЖШЪБЃЌЫФБпаЮOBDCЮЊСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕуAЮЊФГЗтБеЭМаЮБпНчЩЯвЛЖЈЕуЃЌЖЏЕуPДгЕуAГіЗЂЃЌбиЦфБпНчЫГЪБеыдШЫйдЫЖЏвЛжмЃЎЩшЕуPдЫЖЏЕФЪБМфЮЊxЃЌЯпЖЮAPЕФГЄЮЊyЃЎБэЪОyгыxЕФКЏЪ§ЙиЯЕЕФЭМЯѓДѓжТШчЭМЫљЪОЃЌдђИУЗтБеЭМаЮПЩФмЪЧЃЈ ЃЉ

A.  B.
B.  C.
C.  D.
D. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌMNЮЊвЛЕчЪгЫўЃЌABЪЧЦТНЧЮЊ30ЁуЕФаЁЩНЦТЃЈЕчЪгЫўЕФЕзВПNгыЩНЦТЕФЦТНХAдкЭЌвЛЫЎЦНЯпЩЯЃЌБЛвЛИіШЫЙЄКўИєПЊЃЉЃЌФГЪ§бЇаЫШЄаЁзщзМБИВтСПетзљЕчЪгЫўЕФИпЖШЃЎдкЦТНХAДІВтЕУЫўЖЅMЕФбіНЧЮЊ45ЁуЃЛбизХЩНЦТЯђЩЯаазп40mЕНДяCДІЃЌДЫЪБВтЕУЫўЖЅMЕФбіНЧЮЊ30ЁуЃЌЧыЧѓГіЕчЪгЫўMNЕФИпЖШЃЎЃЈВЮПМЪ§ОнЃК![]() Ёж1.41ЃЌ
Ёж1.41ЃЌ![]() Ёж1.73ЃЌНсЙћБЃСєећЪ§ЃЉ
Ёж1.73ЃЌНсЙћБЃСєећЪ§ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввЁЂБћ3УћбЇЩњИїздЫцЛњбЁдёЕНAЁЂBСНИіЪщЕъЙКЪщ.
(1)дђМзЁЂвв2УћбЇЩњдкВЛЭЌЪщЕъЙКЪщЕФИХТЪЪЧ________ЃЛ
(2)ЧѓМзЁЂввЁЂБћ3УћбЇЩњдкЭЌвЛЪщЕъЙКЪщЕФИХТЪ.
(ЧыгУЛЁАЪїзДЭМЁБЛђЁАСаБэЁБЕШЗНЗЈаДГіНтЬтЙ§ГЬ)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГХЉПЦЫљдкЯрЭЌЬѕМўЯТзіФГжжзїЮяжжзгЗЂбПТЪЕФЪдбщЃЌНсЙћШчЯТБэЫљЪОЃК
жжзгИіЪ§n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
ЗЂбПжжзгИіЪ§m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
ЗЂбПжжзгЦЕТЪ | 0ЃЎ899 | 0ЃЎ910 | 0ЃЎ898 | 0ЃЎ911 | 0ЃЎ909 | 0ЃЎ912 | 0ЃЎ908 | 0ЃЎ910 |
вЛАуЕиЃЌ![]() ИУжжзїЮяжжзгжаДѓдМгаЖрЩйЪЧВЛФмЗЂбПЕФЃП
ИУжжзїЮяжжзгжаДѓдМгаЖрЩйЪЧВЛФмЗЂбПЕФЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌEЁЂFЗжБ№ЮЊDCЁЂDAБпЩЯЕФЕуЃЌЁЯEBFЃН45ЁуЃЌШєEFЃН5ЃЌCEЃН2ЃЌдђе§ЗНаЮABCDЕФБпГЄЮЊ( )

A.8B.6C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
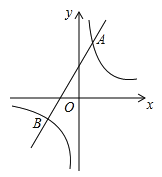
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=k1x+bгыЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓНЛгкAЃЈ2ЃЌmЃЉЃЌBЃЈ-3ЃЌЉ2ЃЉСНЕу.
ЕФЭМЯѓНЛгкAЃЈ2ЃЌmЃЉЃЌBЃЈ-3ЃЌЉ2ЃЉСНЕу.
ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉИљОнЫљИјЬѕМўЃЌЧыжБНгаДГіВЛЕШЪНk1x+bЃО![]() ЕФНтМЏЃЛ
ЕФНтМЏЃЛ
ЃЈ3ЃЉШєPЃЈpЃЌy1ЃЉЃЌQЃЈЉ2ЃЌy2ЃЉЪЧКЏЪ§y=![]() ЭМЯѓЩЯЕФСНЕуЃЌ Чвy1ЃОy2ЃЌЧѓЪЕЪ§pЕФШЁжЕЗЖЮЇ.
ЭМЯѓЩЯЕФСНЕуЃЌ Чвy1ЃОy2ЃЌЧѓЪЕЪ§pЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГХЉВњЦЗЙЋЫОвд![]() дЊЕФГЩБОЪеЙКСЫФГжжХЉВњЦЗ
дЊЕФГЩБОЪеЙКСЫФГжжХЉВњЦЗ![]() ЖжЃЌФПЧАПЩвдвд
ЖжЃЌФПЧАПЩвдвд![]() дЊ/ЖжЕФМлИёжБНгЪлГі.ЖјИУЙЋЫОЖдетХњХЉВњЦЗгавдЯТСНжжДІРэЗНЪНПЩЙЉбЁдёЃК
дЊ/ЖжЕФМлИёжБНгЪлГі.ЖјИУЙЋЫОЖдетХњХЉВњЦЗгавдЯТСНжжДІРэЗНЪНПЩЙЉбЁдёЃК
ЗНЪНвЛЃКЙЋЫОПЩНЋВПЗжХЉВњЦЗжБНгвд![]() дЊ/ЖжЕФМлИёЪлГіЃЌЪЃЯТЕФШЋВПМгЙЄГЩАыГЩЦЗГіЪлЃЈМгЙЄГЩБОКіТдВЛМЦЃЉЃЌУПЖжИУХЉВњЦЗПЩвдМгЙЄЕУЕН
дЊ/ЖжЕФМлИёЪлГіЃЌЪЃЯТЕФШЋВПМгЙЄГЩАыГЩЦЗГіЪлЃЈМгЙЄГЩБОКіТдВЛМЦЃЉЃЌУПЖжИУХЉВњЦЗПЩвдМгЙЄЕУЕН![]() ЖжЕФАыГЩЦЗЃЌУПЖжАыГЩЦЗЕФЪлМлЮЊ
ЖжЕФАыГЩЦЗЃЌУПЖжАыГЩЦЗЕФЪлМлЮЊ![]() дЊ.
дЊ.
ЗНЪНЖўЃКЙЋЫОНЋИУХњХЉВњЦЗШЋВПДЂВиЦ№РДЃЌетбљУПаЧЦкЛсЫ№ЪЇ![]() ЖжЃЌЧвУПаЧЦкашжЇИЖИїжжЗбгУ
ЖжЃЌЧвУПаЧЦкашжЇИЖИїжжЗбгУ![]() дЊЃЌЕЋЭЌЪБУПаЧЦкУПЖжЕФМлИёНЋЩЯеЧ
дЊЃЌЕЋЭЌЪБУПаЧЦкУПЖжЕФМлИёНЋЩЯеЧ![]() дЊ.
дЊ.
ЃЈ1ЃЉШєИУЙЋЫОбЁШЁЗНЪНвЛДІРэИУХњХЉВњЦЗЃЌзюжеЛёЕУСЫ![]() ЕФРћШѓТЪЃЌЧѓИУЙЋЫОжБНгЯњЪлСЫЖрЩйЖжХЉВњЦЗЃП
ЕФРћШѓТЪЃЌЧѓИУЙЋЫОжБНгЯњЪлСЫЖрЩйЖжХЉВњЦЗЃП
ЃЈ2ЃЉШєИУЙЋЫОбЁШЁЗНЪНЖўДІРэИУХњХЉВњЦЗЃЌзюжеЛёРћ1![]() дЊЃЌЧѓИУХњХЉВњЦЗДЂВиСЫЖрЩйИіаЧЦкВХГіЪлЃП
дЊЃЌЧѓИУХњХЉВњЦЗДЂВиСЫЖрЩйИіаЧЦкВХГіЪлЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com