
 一张矩形纸片ABCD的边长分别为9厘米和3厘米,把顶点A和C叠合在一起,得到折痕EF.
一张矩形纸片ABCD的边长分别为9厘米和3厘米,把顶点A和C叠合在一起,得到折痕EF.分析 (1)先根据平行四边形的判定定理求出四边形AECF是平行四边形,再根据AF=CF即可求出答案;
(2)根据图形折叠的性质可得到AF=CF,设AF=x,则CF=x,BF=9-x,在Rt△BCF中,利用勾股定理即可求出CF、BF的长,过E作EM⊥AB交AB于M,在Rt△EMF中利用勾股定理即可求出EF的长;
(3)根据对称的性质可知△CEH≌△AED,再由三角形的面积公式即可求解.
解答 解:(1)如图,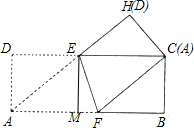
∵AB∥CD,
∴AF∥CE,CF∥HE,
根据对称性,知∠CEH=∠AED,
∵D、E、C三点共线,
∴A、E、H三点共线,
∴AE∥CF,
∴四边形AECF是平行四边形,
又∵AF=CF,
∴四边形AECF是菱形;
(2)设AF=x,则CF=x,BF=9-x.
在△BCF中,CF2=BF2+BC2,
∴x2=(9-x)2+32,
解得x=5,即CF=5,BF=4.
过E作EM⊥AB交AB于M,则MF=BM-BF=CE-BF=CF-BF=1,
EM=3.
∴$EF=\sqrt{E{M}^{2}+M{F}^{2}}=\sqrt{10}$;
(3)根据对称性,知△CEH≌△AED,
所以S△CEH=S△AED=$\frac{1}{2}$DE•AD=$\frac{1}{2}$(AF-MF)•AD=$\frac{1}{2}$×4×3=6(cm2).
点评 本题考查的是图形折叠的性质及勾股定理,解答此类问题时首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件.解题时,我们常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:选择题
| A. | 为了解10000个灯泡的使用寿命,选择普查 | |
| B. | 为了解某鱼塘中鱼的质量,选择普查 | |
| C. | 为了解某班级学生的视力情况,选择普查 | |
| D. | 为了解一批袋装食品是否有防腐剂,选择普查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
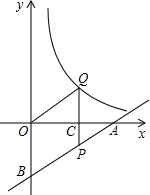 如图,一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=$\frac{k}{x}$(k>0)的图象于Q,S△OQC=$\frac{3}{2}$,则k的值是3;Q点的坐标分别为(2,$\frac{3}{2}$).
如图,一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=$\frac{k}{x}$(k>0)的图象于Q,S△OQC=$\frac{3}{2}$,则k的值是3;Q点的坐标分别为(2,$\frac{3}{2}$).查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中复习检测数学试卷(一)(解析版) 题型:单选题
下列计算错误的是( )
A. (-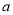 )2·(-
)2·(-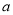 )=-
)=-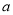 3 B.
3 B. 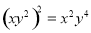 C.
C. 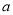 7÷
7÷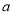 7=1 D. 2
7=1 D. 2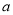 4·3
4·3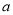 2=6
2=6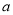 8
8
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
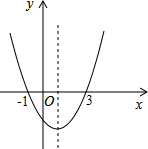 如图二次函数y=ax2+bx+c的图象与x轴交于(-1,0 ),(3,0);下列说法正确的是( )
如图二次函数y=ax2+bx+c的图象与x轴交于(-1,0 ),(3,0);下列说法正确的是( )| A. | abc<0 | B. | 当x>1时,y随x值的增大而增大 | ||
| C. | a+b+c>0 | D. | 当y>0时,-1<x<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com