
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于点M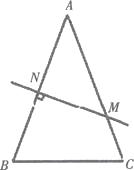
(1)若∠B=70。 , 求∠NMA.
(2)连接MB,若AB=8cm,△MBC的周长是14cm,求BC的长.
(3)在(2)的条件,直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
【答案】
(1)解:∵AB=AC
∴∠B=∠C=70°
∴∠A=180°-∠B-∠C=180°-2 × 70°=40°
∵MN垂直平分AB,
∴∠ANM=90°
∴∠NMA=90°-∠A=90°-40°=50°
(2)解:(2)如图1,连接BM 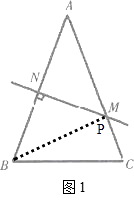
∵AB=AC,AB=8cm
∴AC=8
∵MN垂直平分AB,
∴AM=BM
∵△MBC的周长是14cm
∴BM+CM+BC=14,
∴AM+CM+BC=14,
即AC+BC=14
∴BC=14-8=6
(3)存在;点P与点M重合;△PBC的周长最小值为14.
解:(3)如图1,∵MN垂直平分AB,
∴点A、B关于直线MN对称,AC与MN交于点M,因此点M与点P重合
∴PB+PC的值最小。
∴△PBC的周长最小值为14.
【解析】(1)根据等边对等角求出∠C的度数,再根据三角形的内角和定理求出∠A的度数,再根据垂线的定义得出∠ANM=90°,然后根据∠NMA=90°-∠A,计算即可得出答案。
(2)根据相等垂直平分线的性质得出AM=BM,再根据△MBC的周长是14cm,证得AC+BC=14 ,即可得出答案。
(3)根据轴对称的性质及两点之间的最短,可得出点P与点M重合,因此△PBC的周长最小值就是△MBC的周长。


科目:初中数学 来源: 题型:
【题目】今年参加我市初中毕业生学业考试的总人数约为56000人,这个数据用科学记数法表示为( )
A.5.6×103
B.5.6×104
C.5.6×105
D.0.56×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=![]() ,∠DPA=45°.
,∠DPA=45°.
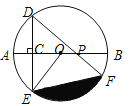
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,D为BC的中点,以下结论:①△ABD≌△ACD;②AB=AC;③∠B=∠C;④AD是△ABC的角平分线.其中正确的有( )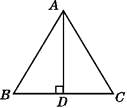
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的个数为( )
①在同一平面内不相交的两条直线叫做平行线;②平面内经过一点有且只有一条直线与已知直线垂直;③经过一点有且只有一条直线与已知直线平行;
④平行同一直线的两直线平行.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com