
 在数轴上,点A向右移动1个单位得到点B,点B向右移动(n+1)(n为正整数)个单位得到点C,点A、B、C分别表示有理数a、b、c.
在数轴上,点A向右移动1个单位得到点B,点B向右移动(n+1)(n为正整数)个单位得到点C,点A、B、C分别表示有理数a、b、c.| n+2 |
| 2 |
| n+3 |
| 2 |
| n+3 |
| 2 |
| n+2 |
| 2 |
| 3 |
| 2 |


科目:初中数学 来源: 题型:
 如图,蒙古包可以近似地看作由圆锥和圆柱组成的,现想用毛毡搭建底面积为9πm2,高为6m,外围高为2m的蒙古包,求至少需要多少平方米的毛毡?(结果保留π)
如图,蒙古包可以近似地看作由圆锥和圆柱组成的,现想用毛毡搭建底面积为9πm2,高为6m,外围高为2m的蒙古包,求至少需要多少平方米的毛毡?(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 0.52 |
| 4 |
| -32 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、8654×108元 |
| B、8.654×109元 |
| C、8.654×1010元 |
| D、0.8654×1011元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
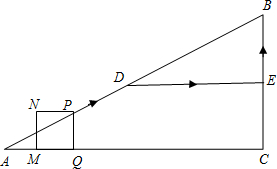 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,D、E分别为边AB、BC的中点,连结DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,D、E分别为边AB、BC的中点,连结DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在AD上以| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 小明骑车外出,所行的路程S(千米)与时间t(小时)的关系如图所示,现有下列四种说法:
小明骑车外出,所行的路程S(千米)与时间t(小时)的关系如图所示,现有下列四种说法:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com