
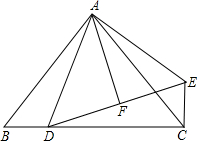
 △ABC中,AB=AC,∠BAC=90°,D是BC上一点,F是DE上一点,且EC⊥BC,EC=BD,DF=FE
△ABC中,AB=AC,∠BAC=90°,D是BC上一点,F是DE上一点,且EC⊥BC,EC=BD,DF=FE分析 (1)证出∠B=∠ACE,由SAS证明三角形全等即可;
(2)利用(1)的结论△ABD≌△ACE得出AD=AE,∩BAD=∩CAE,证出∠ADE是直角三角形,在等腰三角形ADE中,又因为DF=EF,所以可利用等腰三角形的三线合一的性质得出结论AF⊥DE,求出DE=2AF=10,即可得出△ADE的面积.
解答 (1)证明:∵AB=AC,∠BAC=90°,∴∠B=∠BCA=45°.
又∵EC⊥BC,
∴∠ACE=90°-45°=45°.
∴∠B=∠ACE.
在△ABD与△ACE中,$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠B=∠ACE}&{\;}\\{DB=EC}&{\;}\end{array}\right.$,
∴△ABD≌△ACE(SAS).
(2)解:由(1)知△ABD≌△ACE,
∴AD=AE.∠BAD=∠CAE,
∵∠BAC=90°,
∴∠DAE=90°,
等腰△ADE中,DF=EF,
∴AF⊥DE,DE=2DF=10,
∴△ADE的面积=$\frac{1}{2}$DE•AF=$\frac{1}{2}$×10×5=25.
点评 本题考查了全等三角形的判定和性质;三角形全等的问题要找准三角形中现有的条件然后找需要的条件,根据所给出的已知条件结合图形得出所需条件.等腰三角形中三线合一是非常重要的.注意应用.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:选择题
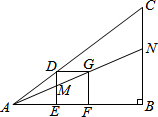 如图△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AC=5,BC=3,DG=1,则BN的长度为( )
如图△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AC=5,BC=3,DG=1,则BN的长度为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{8}{5}$ | D. | $\frac{12}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
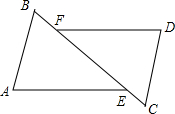 如图,AB=DC,BF=CE,需要补充一个条件,就能使△ABE≌△DCF,小明给出了四个答案::①AE=DF;②AE∥DF;③AB∥DC;④∠A=∠D,其中正确的是( )
如图,AB=DC,BF=CE,需要补充一个条件,就能使△ABE≌△DCF,小明给出了四个答案::①AE=DF;②AE∥DF;③AB∥DC;④∠A=∠D,其中正确的是( )| A. | ①③ | B. | ①② | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}+\frac{1}{2}=-2$ | B. | $(-\frac{1}{3}{)^2}=\frac{1}{9}$ | C. | |3|=3 | D. | $\sqrt{12}=2\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
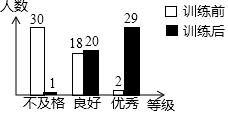 某校九年级700名学生在2016年中考体育考试前对跑步进行了强化训练,在训练前后进行了二次测试,测试成绩都以同一标准(10分为满分)划分成“不及格(7分及以下)”、“良好(9分或8分)”和“优秀(10分)”三个等级.为了了解强化训练的效果,用随机方式抽取了九年级学生中50名学生的前后两次测试成绩的等级,并绘制成如图所示的统计图,试结合图形信息回答下列问题:
某校九年级700名学生在2016年中考体育考试前对跑步进行了强化训练,在训练前后进行了二次测试,测试成绩都以同一标准(10分为满分)划分成“不及格(7分及以下)”、“良好(9分或8分)”和“优秀(10分)”三个等级.为了了解强化训练的效果,用随机方式抽取了九年级学生中50名学生的前后两次测试成绩的等级,并绘制成如图所示的统计图,试结合图形信息回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com