
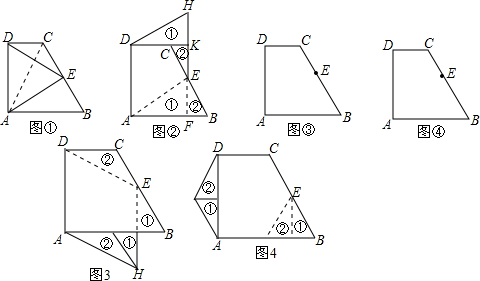
���� ��1����E��BC���е㣬��CEA=90�㣬�õ�AE��ֱƽ��BC���ɵ��������ε����ʵõ���BAE=��CAE�����۵������ʵá�CAE=��DAC�����ǵõ����ۣ�
��2��֤�á�ABC�ǵȱ������Σ������Ǻ������ɵĽ����
��3���ı���HDAE�����Σ��������ƴͼ��֪����H��K��E���ߣ�HE���ı���HDAE��һ�ߣ���ƽ�Ƶõ���BFE�ա�CKE����AFE��DKH�����۵������ʿ�֪��AD=AE���Ƴ�AE=DH=AD=HE������֤�ý��ۣ�
��4����ͼ��ʾ������AHED����������AFECDG��Ϊ����
��� ��1��֤������DC��AB����DAB=90�㣬
���ADC=90�㣬
���۵������ʵã���AEC=��ADC=90�㣬
���CEA=90�㣬
��E��BC���е㣬
��AE��ֱƽ��BC��
��AC=AB��
���BAE=��CAE��
���۵������ʵã���CAE=��DAC��
���DAC=��EAB��
��2���⣺��CD��AB����DAB=��CDA=90�㣬
���DAC=$\frac{1}{3}$��DAB=30�㣬
���CAB=60�㣬
���ABC�ǵȱ������Σ�
��Rt��ADC����CD=10��
��AC=20��AD=10$\sqrt{3}$��
��BC=AC=20cm��
��3���ı���HDAE�����Σ�
֤�����������ƴͼ��֪����H��K��E���ߣ�HE���ı���HDAE��һ�ߣ���BFE�ա�CKE����AFE��DKH��
��KH=KE=EF��AE=DH��
�ߡ�EAF=30�㣬��EFA=90�㣬
��AE=2EF=HE��
���۵������ʿ�֪��AD=AE��
��AE=DH=AD=HE��
���ı���HDAE�����Σ�
��4���⣺��ͼ��ʾ������AHED����������AFECDG��Ϊ����
���� ���⿼����ͼ�εı任-�۵���ƽ�ƣ����ε����ʣ��ȱ������ε����ʣ���ȷ��ʶ��ͼ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
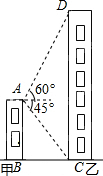 ��ͼ����¥AB�ĸ߶�Ϊ100�ף��Լ�¥¥��A���������¥����D��������Ϊ60�㣬�����¥�ײ�C���ĸ���Ϊ45�㣬����¥CD�ĸ߶ȣ�����������ţ���
��ͼ����¥AB�ĸ߶�Ϊ100�ף��Լ�¥¥��A���������¥����D��������Ϊ60�㣬�����¥�ײ�C���ĸ���Ϊ45�㣬����¥CD�ĸ߶ȣ�����������ţ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
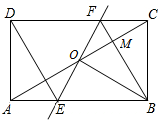 ��ͼ������ABCD�У���OΪAC���е㣬����O��ֱ�߷ֱ���AB��CD���ڵ�E��F������BF��AC�ڵ�M������DE��BO������COB=60�㣬FO=FC����֤��
��ͼ������ABCD�У���OΪAC���е㣬����O��ֱ�߷ֱ���AB��CD���ڵ�E��F������BF��AC�ڵ�M������DE��BO������COB=60�㣬FO=FC����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
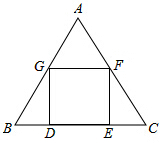 ��ABC��һ��ȱ������εķ���Ƭ�����������һ��������DEFG��ʹ�����ε�һ����DE����BC�ϣ�����F��G�ֱ�����AC��AB�ϣ�
��ABC��һ��ȱ������εķ���Ƭ�����������һ��������DEFG��ʹ�����ε�һ����DE����BC�ϣ�����F��G�ֱ�����AC��AB�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڳ����������У�ÿ��С�����εij�Ϊ2����Ϊ1��A��B�������������ϣ�����CҲ���������ϣ���A��B��CΪ��������������Ϊ1�������������ĵ�C�����ǣ�������
��ͼ���ڳ����������У�ÿ��С�����εij�Ϊ2����Ϊ1��A��B�������������ϣ�����CҲ���������ϣ���A��B��CΪ��������������Ϊ1�������������ĵ�C�����ǣ�������| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com