
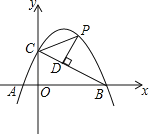
【题目】在平面直角坐标系XOY中,抛物线y=﹣x2+bx+c经过点A(﹣2,0),B(8,0).
(1)求抛物线的解析式;
(2)点C是抛物线与y轴的交点,连接BC,设点P是抛物线上在第一象限内的点,PD⊥BC,垂足为点D.
①是否存在点P,使线段PD的长度最大?若存在,请求出点P的坐标;若不存在,请说明理由;
②当△PDC与△COA相似时,直接写出点P的坐标.
【答案】(1)![]() ;(2)①当P(4,6)时,PD的长度最大,最大值是
;(2)①当P(4,6)时,PD的长度最大,最大值是![]() ;②当△PDC与△COA相似时,点P的坐标为(6,4)或(3,
;②当△PDC与△COA相似时,点P的坐标为(6,4)或(3,![]() ).
).
【解析】
(1)把A(﹣2,0),B(8,0)代入抛物线y=﹣x2+bx+c,即可求解;
(2)①在Rt△PDE中,PD=PEsin∠PED=PEsin∠OCB=![]() PE,即可求解;②分∠PCD=∠CBO、∠PCD=∠BCO两种情况,分别求解.
PE,即可求解;②分∠PCD=∠CBO、∠PCD=∠BCO两种情况,分别求解.
(1)把A(﹣2,0),B(8,0)代入抛物线y=﹣x2+bx+c,![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为:![]() ;
;
(2)由(1)知C(0,4),∵B(8,0),
将点B、C的坐标代入一次函数表达式并解得:
直线BC的解析式为:y=﹣![]() x+4,
x+4,
①如图1,过P作PG⊥x轴于G,PG交BC于E,
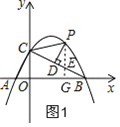
Rt△BOC中,OC=4,OB=8,
∴BC=![]() ,
,
在Rt△PDE中,PD=PEsin∠PED=PEsin∠OCB=![]() PE,
PE,
∴当线段PE最长时,PD的长最大,
设P(t,![]() ),则E(t,﹣
),则E(t,﹣![]() t+4),
t+4),
∴PE=PG﹣EG=![]() ,(0<t<8),
,(0<t<8),
当t=4时,PE有最大值是4,此时P(4,6),
∴PD═![]() ,
,
即当P(4,6)时,PD的长度最大,最大值是![]() ;
;
②∵A(﹣2,0),B(8,0),C(0,4),
∴OA=2,OB=8,OC=4,
∴AC2=22+42=20,AB2=(2+8)2=100,BC2=42+82=80,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴△COA∽△BOC,
当△PDC与△COA相似时,就有△PDC与△BOC相似,
∵相似三角形的对应角相等,
∴∠PCD=∠CBO或∠PCD=∠BCO,
(I)若∠PCD=∠CBO时,即Rt△PDC∽Rt△COB,
此时CP∥OB,
∵C(0,4),
∴yP=4,
∴![]() =4,
=4,
解得:x1=6,x2=0(舍),
即Rt△PDC∽Rt△COB时,P(6,4);
(II)若∠PCD=∠BCO时,
即Rt△PDC∽Rt△BOC,
如图2,过P作x轴的垂线PG,交直线BC于F,
∴PF∥OC,
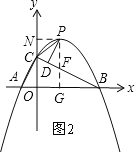
∴∠PFC=∠BCO,
∴∠PCD=∠PFC,
∴PC=PF,
设P(n,![]() ),则PF=﹣
),则PF=﹣![]() n2+2n,
n2+2n,
过P作PN⊥y轴于N,
Rt△PNC中,PC2=PN2+CN2=PF2,
∴n2+(![]() ﹣4)2=(﹣
﹣4)2=(﹣![]() n2+2n)2,
n2+2n)2,
解得:n=3,
即Rt△PDC∽Rt△BOC时,P(3,![]() );
);
综上所述,当△PDC与△COA相似时,点P的坐标为(6,4)或(3,![]() ).
).


科目:初中数学 来源: 题型:
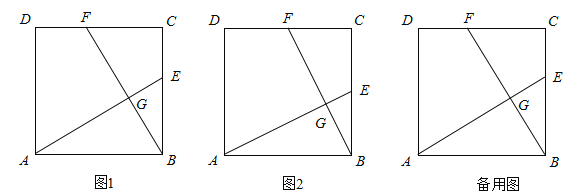
【题目】正方形ABCD的边长为4,点E在BC上,点F在CD上,且CF=BE,AE与BF交于G点.
(1)如图1,求证:①AE=BF,②AE⊥BF.
(2)连接CG并延长交AB于点H,
①若点E为BC的中点(如图2),求BH的长;
②若点E在BC的边上滑动(不与B、C重合),当CG取得最小值时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小张把容积为60升的油箱加满后自驾出行,行驶一段路程后进入服务区停车休息,休息后,小张离开服务区继续前行,为能顺利到达目的地,小张需在相距S千米的加油站加油.若小张从出发点到服务区休息点行驶的路程为200千米,且这期间平均油耗为每千米0.12升.
(1)求小张离开服务区休息点时,油箱内还有多少升汽油?
(2)记小张从离开服务区休息点到进入加油站加油期间的平均油耗为每千米a升,请写出S与a的函数关系式;若0.08≤a≤0.1,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.

(1)在平面直角坐标系中画出探险路线图;
(2)分别写出A、B、C、D、P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,E是AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止;点Q从点B沿BC运动到点C时停止,速度均为每秒1个单位长度.如果点P、Q同时开始运动,设运动时间为t,△BPQ的面积为y,已知y与t的函数图象如图②所示,以下结论:①BC=10;②cos∠ABE=![]() ;③当0≤t≤10时,y=
;③当0≤t≤10时,y=![]() t2;④当t=12时,△BPQ是等腰三角形;⑤当14≤t≤20时,y=110﹣5t,其中正确的有( )
t2;④当t=12时,△BPQ是等腰三角形;⑤当14≤t≤20时,y=110﹣5t,其中正确的有( )
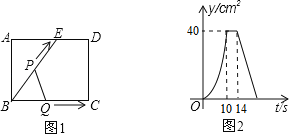
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学考试中,小明有一道选择题(只能在四个选项A、B、C、D中选一个)不会做,便随机选了一个答案;小亮有两道选择题都不会做,他也随机选了两个答案.
(1)小明随机选的这个答案,答对的概率是 ;
(2)通过画树状图或列表法求小亮两题都答对概率是多少?
(3)这个班数学老师参加集体阅卷,在阅卷的过程中,发现学生的错误率较高.他想:若这10道选择题都是靠随机选择答案,则这10道选择题全对的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )

A. 1<MN<5 B. 1<MN≤5 C. ![]() <MN<
<MN<![]() D.
D. ![]() <MN≤
<MN≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知抛物线y=﹣x2+(1﹣m)x﹣m2+12交x轴于点A,交y轴于点B(0,3),顶点C位于第二象限,连接AB,AC,BC.
(1)求抛物线的解析式;
(2)在x轴上是否存在点P,使得△PAB的面积等于△ABC的面积?如果存在,求出点P的坐标.
(3)将△ABC沿x轴向右移动t个单位长度(0<t<1)时,平移后△ABC和△ABO重叠部分的面积为S,求S与t之间的函数关系.
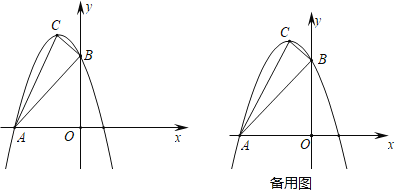
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com