
【题目】近段时间共享单车风靡全国,刺激了自行车生产厂家,某厂家准备生产![]() 两种型号的共享单车,已知生产6辆
两种型号的共享单车,已知生产6辆![]() 型单车与5辆
型单车与5辆![]() 型单车的成本相同,生产3辆
型单车的成本相同,生产3辆![]() 型单车与2辆
型单车与2辆![]() 型单车共需1080元。
型单车共需1080元。
(1)求生产一辆![]() 型车和生产一辆
型车和生产一辆![]() 型单车的成本各为多少元?
型单车的成本各为多少元?
(2)由于共享单车公司需求量加大,生产厂家需要再生产![]() 两种型号的单车共10000辆,恰逢原料商对基本原料的价格进行调整,调整后,
两种型号的单车共10000辆,恰逢原料商对基本原料的价格进行调整,调整后,![]() 型单车每辆成本价比原来降低10%,
型单车每辆成本价比原来降低10%,![]() 型单车每辆的成本价不变,如果厂家准备投入的总成本不超过216万元,那么至少要生产多少辆
型单车每辆的成本价不变,如果厂家准备投入的总成本不超过216万元,那么至少要生产多少辆![]() 型单车?
型单车?
(3)在(2)的条件下,该生产厂家发现,销售过程中每辆![]() 型单车可获利100元,每辆
型单车可获利100元,每辆![]() 型单车可获利120元,求全部销售完这批单车获得的利润
型单车可获利120元,求全部销售完这批单车获得的利润![]() 与
与![]() 型单车辆数
型单车辆数![]() 之间的函数关系式,并求获利最大的方案及最大利润。
之间的函数关系式,并求获利最大的方案及最大利润。
【答案】(1)![]() 型200元,
型200元, ![]() 型240元.(2)4000辆.(3)
型240元.(2)4000辆.(3)![]() ,生产4000辆
,生产4000辆![]() 型单车、6000辆
型单车、6000辆![]() 型单车时,获得的利润最大,最大值为112万元..
型单车时,获得的利润最大,最大值为112万元..
【解析】
(1)设生产一辆![]() 型单车成本为
型单车成本为![]() 元,生产一辆
元,生产一辆![]() 型单车的成本
型单车的成本![]() 元,根据“生产6辆
元,根据“生产6辆![]() 型单车与5辆
型单车与5辆![]() 型单车的成本相同,生产3辆
型单车的成本相同,生产3辆![]() 型单车与2辆
型单车与2辆![]() 型单车共需1080元”列二元一次方程,并求解即可;
型单车共需1080元”列二元一次方程,并求解即可;
(2)设生产![]() 辆
辆![]() 型单车,则生产
型单车,则生产![]() 型单车
型单车![]() 辆,由题意列一元一次不等式并求解即可;
辆,由题意列一元一次不等式并求解即可;
(3)设该厂获得的总利润为![]() 元,由题意得关于
元,由题意得关于![]() 的函数,并结合一次函数的性质求解即可.
的函数,并结合一次函数的性质求解即可.
解:(1)设生产一辆![]() 型单车成本为
型单车成本为![]() 元,生产一辆
元,生产一辆![]() 型单车的成本
型单车的成本![]() 元,
元,
根据题意得:![]()
解得:![]() .
.
答:生产一辆![]() 型单车成本为200元,生产一辆
型单车成本为200元,生产一辆![]() 型单车的成本240元.
型单车的成本240元.
(2)设生产![]() 辆
辆![]() 型单车,则生产
型单车,则生产![]() 型单车
型单车![]() 辆,由题意得:
辆,由题意得:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
答:至少要生产4000辆![]() 型单车.
型单车.
(3)设该厂获得的总利润为![]() 元,由题意得:
元,由题意得:
![]()
![]()
![]() 的值随
的值随![]() 的增大而减小.
的增大而减小.
![]() 当
当![]() 时,
时,![]() 取最大值,最大值为
取最大值,最大值为![]()
答:生产4000辆![]() 型单车、6000辆
型单车、6000辆![]() 型单车时,获得的利润最大,最大值为112万元.
型单车时,获得的利润最大,最大值为112万元.


科目:初中数学 来源: 题型:
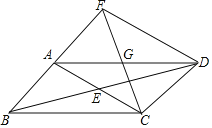
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.请根据图中的信息,解答下列问题:
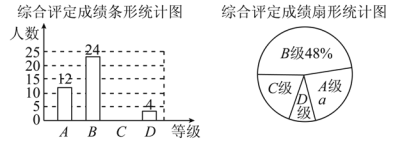
(1)在这次调查中,一共抽取了________名学生,a=________%;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为________度;
(4)若该校共有2 000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把分子为1的分数叫做单位分数,如![]() ,
, ![]() ,
, ![]() ,…任何一个单位分数都可以拆分成两个不同的单位分数的和,如
,…任何一个单位分数都可以拆分成两个不同的单位分数的和,如![]() ,
, ![]() ,
, ![]() ,…
,…
(1)根据对上述式子的观察,你会发现![]() ,则a=________,b=________;
,则a=________,b=________;
(2)进一步思考,单位分数![]() (n是不小于2的正整数),则x=________(用n的代数式表示)
(n是不小于2的正整数),则x=________(用n的代数式表示)
(3)计算: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
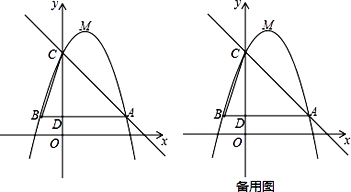
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥ x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ ABC的内部(不包括△ ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△ BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( )
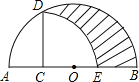
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
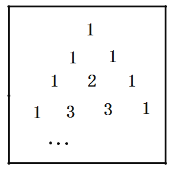
【题目】我国宋朝数学家杨在他的著作《详解九章算法》中提出“杨辉三角”(如图所示),此图揭示了![]() (n为非负整数)展开式的项数及各项系数的有关规律.
(n为非负整数)展开式的项数及各项系数的有关规律.
例如:![]() ,它只有一项,系数为1;
,它只有一项,系数为1;![]() ,它有两项,系数分别为1,1,系数和为2;
,它有两项,系数分别为1,1,系数和为2;![]() ,它有三项,系数分别为1,2,1,系数和为4;
,它有三项,系数分别为1,2,1,系数和为4;![]() ,它有四项系数分别为1,3,3,1,系数和为8;……根据以上规律,解答下列问题:
,它有四项系数分别为1,3,3,1,系数和为8;……根据以上规律,解答下列问题:
(1)![]() 展开式共有________项,系数分别为________.
展开式共有________项,系数分别为________.
(2)![]() 展开式共有________项,系数和为________.
展开式共有________项,系数和为________.
(3)![]() 展开结果为________.
展开结果为________.
(4)利用上面的规律计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和1个B品牌的计算器共需122元;购买1个A品牌和2个B品牌的计算器共需124元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店举行促销活动,具体办法如下:购买A品牌计算器按原价的九折销售,购买B品牌计算器超出10个以上超出的部分按原价的八折销售,①设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
②小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过10个,问购买哪种品牌的计算器更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店经销进价分别为![]() 元/千克、
元/千克、![]() 元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
时间 | 甲水果销量 | 乙水果销量 | 销售收入 |
周五 |
|
|
|
周六 |
|
|
|
(1)求甲、乙两种水果的销售单价;
(2)若水果店准备用不多于![]() 元的资金再购进两种水果共
元的资金再购进两种水果共![]() 千克,求最多能够进甲水果多少千克?
千克,求最多能够进甲水果多少千克?
(3)在(2)的条件下,水果店销售完这![]() 千克水果能否实现利润为
千克水果能否实现利润为![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com