
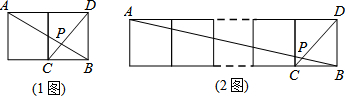
分析 (1)作BH⊥DP于H点,设小正方形的边长为1,根据勾股定理可计算出CD=$\sqrt{2}$,AB=$\sqrt{5}$,再根据三角形面积公式可计算出DH=$\frac{2\sqrt{5}}{5}$,由BC∥AD得到△APD∽△BPC,利用相似比得到PD=2PC,所以PD=$\frac{2}{3}$CD=$\frac{2\sqrt{2}}{3}$,接着在Rt△PHC中,根据勾股定理计算出PH=$\frac{2\sqrt{5}}{15}$,最后利用正切的定义求解.
(2)类比(1)的解题过程,即可解答.
解答 解:作DH⊥BP于H点,如图,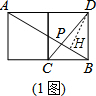
设小正方形的边长为1,则AD=2,
在Rt△BCD中,CD=$\sqrt{{1}^{2}+{1}^{2}}=\sqrt{2}$,
在Rt△ABC中,AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∵$\frac{1}{2}$DH•AB=$\frac{1}{2}$AD•BD,
∴DH=$\frac{2\sqrt{5}}{5}$,
∵AD∥BC,
∴△APD∽△BPC,
∴$\frac{DP}{CP}=\frac{AD}{BC}=\frac{2}{1}$,
即DP=2PC,
∴PD=$\frac{2}{3}$CD=$\frac{2\sqrt{2}}{3}$,
在Rt△PHD中,PH=$\sqrt{P{D}^{2}-D{H}^{2}}$=$\frac{2\sqrt{5}}{15}$,
∴tan∠BPD=$\frac{DH}{PH}$=3.
如果是n个边长为1的正方形组成的n×1格点图,那么tan∠BPD=$\frac{n+1}{n-1}$.
故答案为:3,$\frac{n+1}{n-1}$.
点评 此题考查了相似三角形的判定与性质与三角函数的定义.此题难度适中,解题的关键准确作出辅助线,注意转化思想与数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
 如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
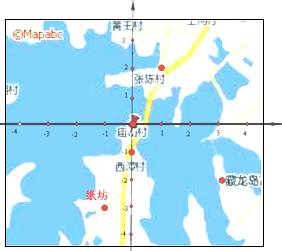
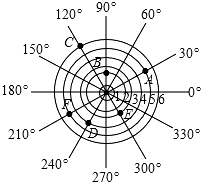 如图,雷达探测器测得六个目标A、B、C、D、E、F出现,按照规定的目标表示方法,目标A、E的位置表示为A(5,30°),E(3,300°),则目标C的位置表示为(6,120°).
如图,雷达探测器测得六个目标A、B、C、D、E、F出现,按照规定的目标表示方法,目标A、E的位置表示为A(5,30°),E(3,300°),则目标C的位置表示为(6,120°).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
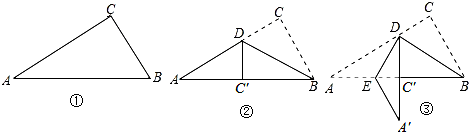
| A. | $2\sqrt{2}$cm | B. | $2\sqrt{3}$cm | C. | $\frac{8}{3}$cm | D. | 3cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
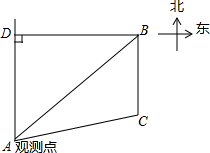 已知B村庄位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为24km,一辆摩托车从B村庄以60km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此摩托车与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,$\sqrt{2}$≈1.41,$\sqrt{5}$≈2.24.
已知B村庄位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为24km,一辆摩托车从B村庄以60km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此摩托车与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,$\sqrt{2}$≈1.41,$\sqrt{5}$≈2.24.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com