
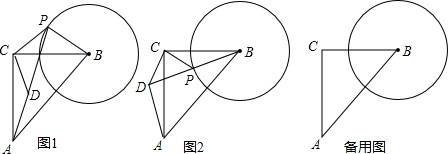
分析 (1)根据SAS即可证明△ACD≌△BCP,再根据全等三角形的性质可得AD=BP;
(2)利用切线的性质结合等腰直角三角形得出即可;
(3)当B、P、D三点在同一条直线上时利用勾股定理,可得BD的长;
(4)当∠PBC=45°时,BD有最小值;进而得出BD有最大值.
解答 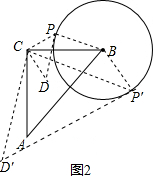
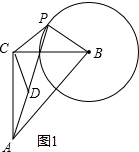 (1)证明:如图1,∵∠ACB=90°,∠DCP=90°,
(1)证明:如图1,∵∠ACB=90°,∠DCP=90°,
∴∠ACD=∠BCP
在△ACD与△BCP中,
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCP}\\{CD=CP}\end{array}\right.$,
∴△ACD≌△BCP(SAS)
∴AD=BP;
(2)解:如图2,∵CP=CD,DP是⊙B的切线,∠PCD=90°,
∴∠BPD=90°,∠ADP=∠APD=45°,
∴∠CPB=45°+90°=135°,
同理可得:∠CPB=45°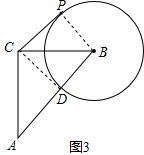
故∠CPB=45°或135°;
故答案为:故∠CPB=45°或135°;
(3)解:∵△CDP为等腰直角三角形,
∴∠CDP=∠CPD=45°,∠CPB=135°,
由(1)知,△ACD≌△BCP,
∴∠CDA=∠CPB=135°,AD=BP=1,
∴∠BDA=∠CDA-∠CDP=90°,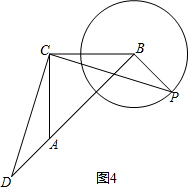
在Rt△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{3}$;
(4)解:如图3,当B、D、A三点在同一条直线上时,BD有最小值,
由(1)得△ACD≌△BCP,
此时∠PBC=45°时,BD的最小值为1,此时tan∠CBP=1;
同理可得:如图4,当B、D、A三点在同一条直线上时,
由(1)得△ACD≌△BCP,BD的最大值为:AB+AD=AB+BP=3,
此时tan∠CBP=tan135°=-1.
故答案为:1,1,3,-1.
点评 此题考查了圆的综合题,涉及的知识有全等三角形的判定与性质,分类思想的运用,最大值与最小值,注意分析问题要全面,以免漏解,有一定的难度.


科目:初中数学 来源: 题型:选择题

| A. | 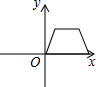 | B. | 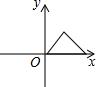 | C. | 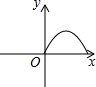 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
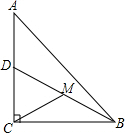 如图,在Rt△ABC中,∠ACB=90°,D为AC的中点,M为BD的中点,将线段AD绕A点任意旋转(旋转过程中始终保持点M为BD的中点),若AC=4,BC=3,那么在旋转过程中,线段CM长度的取值范围是1.5≤CM≤3.5.
如图,在Rt△ABC中,∠ACB=90°,D为AC的中点,M为BD的中点,将线段AD绕A点任意旋转(旋转过程中始终保持点M为BD的中点),若AC=4,BC=3,那么在旋转过程中,线段CM长度的取值范围是1.5≤CM≤3.5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
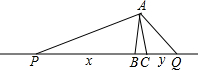 如图,在△ABC中,AB=AC,∠BAC=20°,P,Q在直线BC上,且∠PAQ=100°.设BP=x,CQ=y,则下列结论正确的是( )
如图,在△ABC中,AB=AC,∠BAC=20°,P,Q在直线BC上,且∠PAQ=100°.设BP=x,CQ=y,则下列结论正确的是( )| A. | 当x≠y时,△APB≌△AQC | B. | 当x=y时,∠APB=∠PAB=45° | ||
| C. | 当x=2y时,$\frac{AP}{AQ}$=$\sqrt{2}$ | D. | 当x•y=4时,AB=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
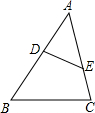 如图,点D、E分别在线段AB、AC上且∠ABC=∠AED,若DE=4,AE=5,BC=8,则AB的长为( )
如图,点D、E分别在线段AB、AC上且∠ABC=∠AED,若DE=4,AE=5,BC=8,则AB的长为( )| A. | $\frac{5}{2}$ | B. | 10 | C. | $\frac{2}{5}$ | D. | $\frac{1}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
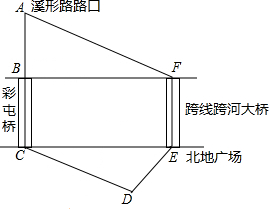 如图,家住彩屯溪形路路口的小李要经过彩屯到北地广场附近上班,路线为A→B→C→D→E.市政府决定修建设北地到彩屯的跨线跨河大桥EF,如果大桥建成后小李就可以由新大桥直线上班,路线A→F→E,BC∥EF,AB⊥BF,DE⊥CD,AB=420米,BC=300米,∠AFB=37°,∠CED=53°,请你帮助计算一下,小李改由新大桥上班会比原先少走多少米?(结果保留整数)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,家住彩屯溪形路路口的小李要经过彩屯到北地广场附近上班,路线为A→B→C→D→E.市政府决定修建设北地到彩屯的跨线跨河大桥EF,如果大桥建成后小李就可以由新大桥直线上班,路线A→F→E,BC∥EF,AB⊥BF,DE⊥CD,AB=420米,BC=300米,∠AFB=37°,∠CED=53°,请你帮助计算一下,小李改由新大桥上班会比原先少走多少米?(结果保留整数)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com