
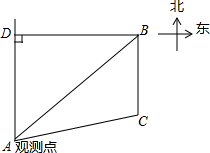
 已知B村庄位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为24km,一辆摩托车从B村庄以60km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此摩托车与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,$\sqrt{2}$≈1.41,$\sqrt{5}$≈2.24.
已知B村庄位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为24km,一辆摩托车从B村庄以60km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此摩托车与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,$\sqrt{2}$≈1.41,$\sqrt{5}$≈2.24. 分析 根据在Rt△ADB中,sin∠DAB=$\frac{DB}{AB}$,得出AB的长,进而得出tan∠BAH=$\frac{BH}{AH}$,求出BH的长,即可得出AH以及CH的长,进而得出答案.
解答 解: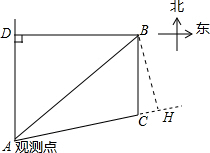 在Rt△ADB中,sin∠DAB=$\frac{DB}{AB}$,sin53.2°≈0.8,
在Rt△ADB中,sin∠DAB=$\frac{DB}{AB}$,sin53.2°≈0.8,
所以AB=$\frac{DB}{sin∠DAB}$≈$\frac{24}{0.8}$=30,
如图,过点B作BH⊥AC,交AC的延长线于H,
在Rt△AHB中,∠BAH=∠DAC-∠DAB=79.8°-53.2°=26.6°,
tan∠BAH=$\frac{BH}{AH}$,
∵tan26.6°≈0.50,
∴0.5=$\frac{BH}{AH}$,
AH=2BH,
BH2+AH2=AB2,BH2+(2BH)2=302,BH=6$\sqrt{5}$,所以AH=12$\sqrt{5}$,
∵摩托车从B村庄以60km/h的速度沿如图所示的BC方向航行,15min后达到C处,
∴BC=60×$\frac{15}{60}$=15km,
∴CH=$\sqrt{B{C}^{2}-B{H}^{2}}$=$\sqrt{1{5}^{2}-(6\sqrt{5})^{2}}$=3$\sqrt{5}$(km)
在Rt△BCH中,BH2+CH2=BC2,CH=3$\sqrt{5}$km,
所以AC=AH-CH=12$\sqrt{5}$-3$\sqrt{5}$=9$\sqrt{5}$≈20.2km,
答:此摩托车与A观测点之间的距离AC的长约为20.2km.
点评 此题主要考查了解直角三角形中方向角问题,根据已知构造直角三角形得出BH的长是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com