
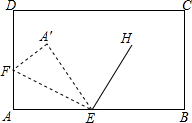
 如图,将一长方形纸片一角斜折,使点A落在A′处,折痕为EF,EH平分∠A′EB,则∠FEH的度数为( )
如图,将一长方形纸片一角斜折,使点A落在A′处,折痕为EF,EH平分∠A′EB,则∠FEH的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 95° |
分析 根据折叠的性质,得∠AEF=∠A′EF,再由角平分线的性质得∠A′EH=∠BEH,则∠FEH=$\frac{1}{2}$(∠AEA′+∠A′EB),即可得出答案.
解答 解:∵将一长方形纸片一角斜折,使点A落在A′处,折痕为EF,EH平分∠A′EB,
∴∠AEF=∠A′EF,∠A′EH=∠BEH,
∴∠FEH=∠A′EF+∠A′EH
=$\frac{1}{2}$∠AEA′+$\frac{1}{2}$∠BEA′,
=$\frac{1}{2}$(∠AEA′+∠A′EB),
=$\frac{1}{2}$×180°
=90°.
故选C.
点评 本题考查了角的计算以及翻折变换,找出折叠后不变的角是解题的关键.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
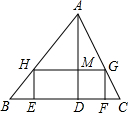 如图,在△ABC中,AD是高,矩形EFGH的顶点H、G分别在AB、AC上,EF在BC上,AD与HG的交点为M.若BC=40cm,AD=30cm,且HG=2HE.则矩形EFGH的周长为72cm.
如图,在△ABC中,AD是高,矩形EFGH的顶点H、G分别在AB、AC上,EF在BC上,AD与HG的交点为M.若BC=40cm,AD=30cm,且HG=2HE.则矩形EFGH的周长为72cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
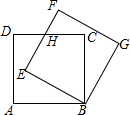 已知如图边长为1cm的两个正方形互相重合,按住其中一个不动,将另一个绕顶点B顺时针旋转30°,则这两个正方形重叠部分的面积是$\frac{\sqrt{3}}{3}$cm2.
已知如图边长为1cm的两个正方形互相重合,按住其中一个不动,将另一个绕顶点B顺时针旋转30°,则这两个正方形重叠部分的面积是$\frac{\sqrt{3}}{3}$cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com