练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．已知正比例函数和反比例函数的图象都经过点（-3，4），求这两个函数的解析式．

    分析 设反比例函数解析式为y=$\frac{k}{x}$，正比例函数解析式为y=k′x，将点（-3，4）代入解析式即可．

    解答 解：设反比例函数解析式为y=$\frac{k}{x}$，
    把点（-3，4）代入解析式得，4=$\frac{k}{-3}$，
    解得k=-12；
    此反比例函数解析式为y=-$\frac{12}{x}$．
    设正比例函数的解析式为y=k′x，
    把点（-3，4）代入解析式得，4=-3k′，
    解得k′=-$\frac{4}{3}$．
    此正比例函数解析式为y=-$\frac{4}{3}$x．

    点评 此题考查了待定系数法求函数解析式，掌握反比例函数和正比例函数的定义正确设出解析式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．为了方便市民的出行，美化海岛公路，某市政府决定给滨海区环岛公路两旁安装路灯，已知需要购买LED路灯250盏，高效节能路灯300盏，共花费29万元，其中，每盏高效节能路灯比每盏LED路灯贵50元．
    （1）每盏LED路灯和高效节能路灯的价格分别是多少元；
    （2）若每盏LED路灯每天耗电1.5度，每盏高效节能路灯每天耗电1度，求环岛公路的路灯一年的电费（一年按365天，当地的电价是0.68元/度）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．计算：（-2a-2）3b2÷2a-4b-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

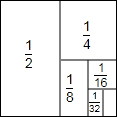    14．阅读材料：如图，把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形（长方形），按着把面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形，再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$ 的矩形，如此进行下去．我们可以利用图形展示的规律将累加式进行化简：$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+A+\frac{1}{{2}^{n}}$．
    例如：由于$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{32}=1$，所以$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}=1-\frac{1}{32}$．
    完成解答：
    ①类比上面推理将累加式$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+A+\frac{1}{{2}^{n}}$化简为1-$\frac{1}{{2}^{n}}$；
    ②利用上面的解题方法化简累加式1+2+22+23+24+A+2n=2n+1-1；
    ③化简累加式：$\frac{5}{2}+\frac{17}{4}+\frac{65}{8}+\frac{257}{16}+…+\frac{（2n）^{2}+1}{{{2}^{n}}_{\;}}$=2n+1-1-$\frac{1}{{2}^{n}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．用“O”摆出如图所示的图案，若按照同样的方式构造图案，则第11个图案需要（　　）个“O”．
    A．100B．145C．181D．221

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

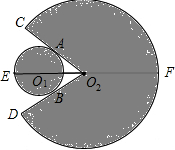    11．【课本知识】用配方法解方程、切线的性质定理、扇形面积公式．
    尝试探究：代数式2x2+4x=2（x2+2x）=2（x2+2x+1-1）=2（x+1）2-2，则当x=-1时，该代数式有最小值，最小值为-2；
    【实际应用】某玩具由一个圆形区域和一个扇形区域组成，如图，在⊙O1和扇形O2CD中，⊙O1与O2C、O2D分别相切于A、B两点，∠CO2D=60°，直线O1O2与⊙O1、扇形O2CD分别交于E、F两点，EF=24cm，设⊙O1的半径为x cm．
    （1）用含x的式子表示扇形O2CD的半径为（24-3x）cm；
    （2）若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元/cm2和0.06元/cm2，当⊙O1的半径为多少时，该玩具的制作成本最小？最小成本为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

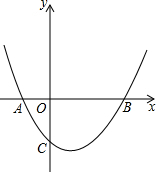    18．如图，经过点A（-1，0），C（0，-2）的抛物线$y=\frac{1}{2}{x^2}+bx+c$与x轴交于A、B两点，与y轴交于点C
    （1）求此抛物线的函数解析式和顶点D的坐标；
    （2）将（1）中求得的抛物线向左平移1个单位长度，再向上平移m（m＞0）个单位长度得到新抛物线y1，若新抛物线y1的顶点P在△ABC内，求m的取值范围；
    （3）在（1）的结论下，在x轴下方的抛物线上是否存在点P，使得∠APB为锐角？若存在，求出点P的横坐标的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知，直线AB、CD被直线EF所截，AB∥CD，点P在直线EF上运动（不含点E、F），点M是AB上固定一点，以PM为始边作∠MPN=60°，交直线CD于点N．
    （1）如图1，猜想并验证∠MPN、∠PMA、∠PNC的数量关系．
    （2）如图2，猜想并验证∠MPN、∠PMA、∠PNC的数量关系．
    （3）如图3，当点P在直线CD下方时，请画出图形，直接写出∠MPN、∠PMA、∠PNC的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．温度通常有两种表示方法：华氏度（单位：℉）与摄氏度（单位：℃），已知华氏度数y与摄氏度数x之间是一次函数关系，如表列出了部分华氏度与摄氏度之间的对应关系：
    摄氏度数x（℃）…0…35…100…
    华氏度数y（℉）…32…95…212…
    （1）选用表格中给出的数据，求y关于x的函数解析式（不需要写出该函数的定义域）；
    （2）已知某天的最低气温是-5℃，求与之对应的华氏度数．

    查看答案和解析>>

    同步练习册答案