
 【课本知识】用配方法解方程、切线的性质定理、扇形面积公式.
【课本知识】用配方法解方程、切线的性质定理、扇形面积公式.分析 尝试探究:直接利用偶次方的性质得出答案;
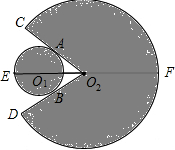
【实际应用】(1)连接O1A.利用切线的性质知∠AO2O1=$\frac{1}{2}$∠CO2D=30°;然后在Rt△O1AO2中利用“30°角所对的直角边是斜边的一半”求得O1O2=2x;最后由图形中线段间的和差关系求得扇形O2CD的半径FO2为:EF-EO1-O1O2=24-3x;
(2)设该玩具的制作成本为y元,则根据圆形的面积公式和扇形的面积公式列出y与x间的函数关系,然后利用二次函数的最值即可求得该玩具的最小制作成本.
解答 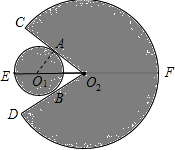 解:尝试探究:代数式2x2+4x=2(x2+2x)=2(x2+2x+1-1)=2(x+1)2-2,
解:尝试探究:代数式2x2+4x=2(x2+2x)=2(x2+2x+1-1)=2(x+1)2-2,
则当x=-1时,该代数式有最小值,最小值为:-2;
故答案为:-1,-2.
【实际应用】(1)连接O1A.
∵⊙O1与O2C、O2D分别切一点A、B
∴O1A⊥O2C,O2E平分∠CO2D,
∴∠AO2O1=$\frac{1}{2}$∠CO2D=30°,
∴在Rt△O1AO2中,O1O2=2AO1=2x.
∴FO2=EF-EO1-O1O2=24-3x,即扇形O2CD的半径为(24-3x)cm.
故答案为:(24-3x);
(2)设该玩具的制作成本为y元,则
y=0.45πx2+0.06×$\frac{(360-60)π×(24-3x)^{2}}{360}$
=0.9πx2-7.2πx+28.8π
=0.9π(x-4)2+14.4π
所以当x-4=0,即x=4时,y的值最小.
答:当⊙O1的半径为4cm时,该玩具的制作成本最小.
点评 本题考查了切线的性质、扇形面积的计算、解直角三角形以及二次函数的最值.在利用二次函数求最值时,此题采用了配方法.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
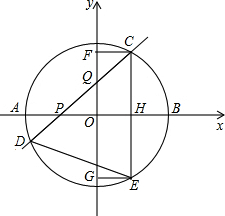 如图,⊙O的圆心O在坐标原点,直径AB=8,点P是直径AB上的一个动点(点P不与A、B两点重合),过点P的直线PQ的解析式为y=x+m,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
如图,⊙O的圆心O在坐标原点,直径AB=8,点P是直径AB上的一个动点(点P不与A、B两点重合),过点P的直线PQ的解析式为y=x+m,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,且点A的坐标为(-3,0),点C坐标为(0,$\sqrt{3}$),点B在y轴的负半轴上,抛物线y=-$\frac{\sqrt{3}}{3}$x2+bx+c经过点A和点C
如图,在△ABC中,AB=AC,且点A的坐标为(-3,0),点C坐标为(0,$\sqrt{3}$),点B在y轴的负半轴上,抛物线y=-$\frac{\sqrt{3}}{3}$x2+bx+c经过点A和点C查看答案和解析>>
科目:初中数学 来源: 题型:解答题
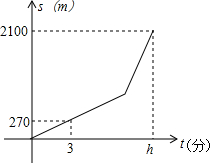 小明从家到学校,开始步行,后来跑步,小明离家的路程S(m)与所用时间t(分)之间的关系如图所示.
小明从家到学校,开始步行,后来跑步,小明离家的路程S(m)与所用时间t(分)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
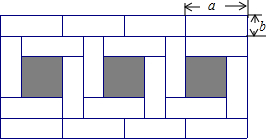 已知将同样大小的小长方形纸片拼成的如图形状的大长方形(小长方形纸片长为a,宽为b)请你仔细观察图形,解答下列问题:
已知将同样大小的小长方形纸片拼成的如图形状的大长方形(小长方形纸片长为a,宽为b)请你仔细观察图形,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
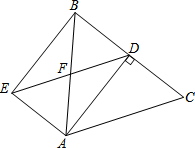 如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积.
如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com