
【题目】如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE= ![]() ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).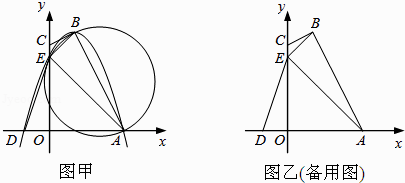
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
【答案】
(1)
解:由题意,设抛物线解析式为y=a(x﹣3)(x+1).
将E(0,3)代入上式,解得:a=﹣1.
∴y=﹣x2+2x+3.
则点B(1,4)
(2)
证明:如图1,过点B作BM⊥y于点M,则M(0,4).

在Rt△AOE中,OA=OE=3,
∴∠1=∠2=45°,AE= ![]() =3
=3 ![]() .
.
在Rt△EMB中,EM=OM﹣OE=1=BM,
∴∠MEB=∠MBE=45°,BE= ![]() =
= ![]() .
.
∴∠BEA=180°﹣∠1﹣∠MEB=90°.
∴AB是△ABE外接圆的直径.
在Rt△ABE中,tan∠BAE= ![]() =
= ![]() =tan∠CBE,
=tan∠CBE,
∴∠BAE=∠CBE.
在Rt△ABE中,∠BAE+∠3=90°,∴∠CBE+∠3=90°.
∴∠CBA=90°,即CB⊥AB.
∴CB是△ABE外接圆的切线.
(3)
解:Rt△ABE中,∠AEB=90°,tan∠BAE= ![]() ,sin∠BAE=
,sin∠BAE= ![]() ,cos∠BAE=
,cos∠BAE= ![]() ;
;
若以D、E、P为顶点的三角形与△ABE相似,则△DEP必为直角三角形;
①DE为斜边时,P1在x轴上,此时P1与O重合;
由D(﹣1,0)、E(0,3),得OD=1、OE=3,即tan∠DEO= ![]() =tan∠BAE,即∠DEO=∠BAE
=tan∠BAE,即∠DEO=∠BAE
满足△DEO∽△BAE的条件,因此 O点是符合条件的P1点,坐标为(0,0).
②DE为短直角边时,P2在x轴上;
若以D、E、P为顶点的三角形与△ABE相似,则∠DEP2=∠AEB=90°,sin∠DP2E=sin∠BAE= ![]() ;
;
而DE= ![]() =
= ![]() ,则DP2=DE÷sin∠DP2E=
,则DP2=DE÷sin∠DP2E= ![]() ÷
÷ ![]() =10,OP2=DP2﹣OD=9
=10,OP2=DP2﹣OD=9
即:P2(9,0);
③DE为长直角边时,点P3在y轴上;
若以D、E、P为顶点的三角形与△ABE相似,则∠EDP3=∠AEB=90°,cos∠DEP3=cos∠BAE= ![]() ;
;
则EP3=DE÷cos∠DEP3= ![]() ÷
÷ ![]() =
= ![]() ,OP3=EP3﹣OE=
,OP3=EP3﹣OE= ![]() span> ;
span> ;
综上,得:P1(0,0),P2(9,0),P3(0,﹣ ![]() ).
).
(4)
解:设直线AB的解析式为y=kx+b.
将A(3,0),B(1,4)代入,得 ![]() ,解得
,解得 ![]() .
.
∴y=﹣2x+6.
过点E作射线EF//x轴交AB于点F,当y=3时,得x= ![]() ,∴F(
,∴F( ![]() ,3).
,3).
情况一:如图2,当0<t≤ ![]() 时,设△AOE平移到△GNM的位置,MG交AB于点H,MN交AE于点S.
时,设△AOE平移到△GNM的位置,MG交AB于点H,MN交AE于点S.
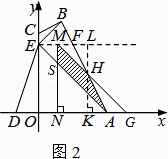
则ON=AG=t,过点H作LK⊥x轴于点K,交EF于点L.
由△AHG∽△FHM,得 ![]() ,即
,即 ![]() .
.
解得HK=2t.
∴S阴=S△MNG﹣S△SNA﹣S△HAG= ![]() ×3×3﹣
×3×3﹣ ![]() (3﹣t)2﹣
(3﹣t)2﹣ ![]() t2t=﹣
t2t=﹣ ![]() t2+3t.
t2+3t.
情况二:如图3,当 ![]() <t≤3时,设△AOE平移到△PQR的位置,PQ交AB于点I,交AE于点V.
<t≤3时,设△AOE平移到△PQR的位置,PQ交AB于点I,交AE于点V.
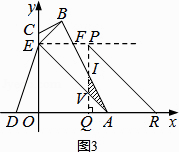
由△IQA∽△IPF,得 ![]() .即
.即 ![]() ,
,
解得IQ=2(3﹣t).
∵AQ=VQ=3﹣t,
∴S阴= ![]() IVAQ=
IVAQ= ![]() (3﹣t)2=
(3﹣t)2= ![]() t2﹣3t+
t2﹣3t+ ![]() .
.
综上所述:s= 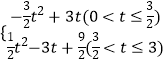 .
.
【解析】(1)已知A、D、E三点的坐标,利用待定系数法可确定抛物线的解析式,进而能得到顶点B的坐标.(2)过B作BM⊥y轴于M,由A、B、E三点坐标,可判断出△BME、△AOE都为等腰直角三角形,易证得∠BEA=90°,即△ABE是直角三角形,而AB是△ABE外接圆的直径,因此只需证明AB与CB垂直即可.BE、AE长易得,能求出tan∠BAE的值,结合tan∠CBE的值,可得到∠CBE=∠BAE,由此证得∠CBA=∠CBE+∠ABE=∠BAE+∠ABE=90°,此题得证.(3)△ABE中,∠AEB=90°,tan∠BAE= ![]() ,即AE=3BE,若以D、E、P为点的三角形与△ABE相似,那么该三角形必须满足两个条件:①有一个角是直角、②两直角边满足1:3的比例关系;然后分情况进行求解即可.(4)过E作EF//x轴交AB于F,当E点运动在EF之间时,△AOE与△ABE重叠部分是个四边形;当E点运动到F点右侧时,△AOE与△ABE重叠部分是个三角形.按上述两种情况按图形之间的和差关系进行求解.
,即AE=3BE,若以D、E、P为点的三角形与△ABE相似,那么该三角形必须满足两个条件:①有一个角是直角、②两直角边满足1:3的比例关系;然后分情况进行求解即可.(4)过E作EF//x轴交AB于F,当E点运动在EF之间时,△AOE与△ABE重叠部分是个四边形;当E点运动到F点右侧时,△AOE与△ABE重叠部分是个三角形.按上述两种情况按图形之间的和差关系进行求解.


科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC与BD相交于O,不能判定四边形ABCD是平行四边形的是( )
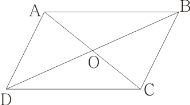
A. AB∥CD,AO=CO B. AB∥DC,∠ABC=∠ADC
C. AB=DC,AD=BC D. AB=DC,∠ABC=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:

小凯的作法如下:
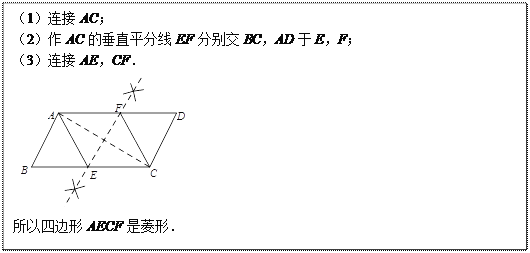
老师说:“小凯的作法正确.”
请回答:在小凯的作法中,判定四边形AECF是菱形的依据是______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长分别为1和2,另一种纸片的两条直角边长都为2.

图1、图2、图3是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1. 请用三种方法将图中所给四块直角三角形纸片全部用上,互不重叠且不留空隙,三种方法所拼得的平行四边形(非矩形)的周长互不相等,并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上.
要求:(1)所画图形各顶点必须与方格纸中的小正方形顶点重合;



(2)画图时,要保留四块直角三角形纸片的拼接痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:
不成立,但有些数可以使得它成立,例如: ![]() .我们称使得
.我们称使得![]() 成立的一对数
成立的一对数![]() ,
, ![]() 为“相伴数对”,记为
为“相伴数对”,记为![]() .
.
(1)若![]() 是“相伴数对”,求
是“相伴数对”,求![]() 的值;
的值;
(2)写出一个“相伴数对” ![]() ,其中
,其中![]() 且
且![]() ;
;
(3)若![]() 是“相伴数对”,求代数式
是“相伴数对”,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图②的极坐标系下,如果正六边形的边长为2,有一边OA在射线ON上,则正六边形的顶点C的极坐标应记为( )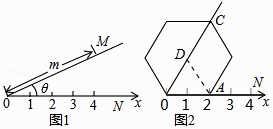
A.(4,60°)
B.(4,45°)
C.(2 ![]() ,60°)
,60°)
D.(2 ![]() ,50°)
,50°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行摸排游戏,现有三张形状大小完全相同的牌,正面分别标有数字2,3,5,将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法写出所有可能的结果;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
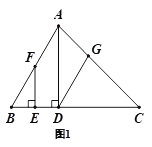
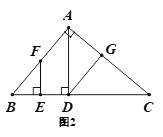
【题目】已知,在三角形ABC中,AD⊥BC于D,F是AB上一点,FE⊥BC于E,∠ADG=∠BFE
(1)如图1,求证:DG∥AB
(2)如图2,若∠BAC=90°,请直接写出图中与∠CAD互余的角,不需要证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com