
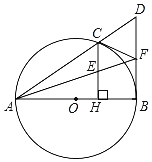
【题目】如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,连接CF.
(1)求证:CF=BF;
(2)求证:CF是⊙O的切线;
(3)若FB=FE=3,求⊙O的半径.
【答案】(1)详见解析;(2)详见解析;(3)6![]() .
.
【解析】
(1)连接OC,BC,证△AEC∽△AFD,△AHE∽△ABF,推出BF=DF,根据直角三角形斜边上中线性质得出CF=DF=BF即可;
(2)证明∠FCB=∠CAB即可推出CF是⊙O的切线;
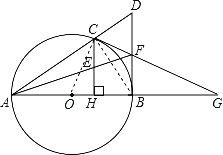
(3)分别延长CF和AB交于点G,∠G=∠FAG,推出AF=FG,求出AB=BG,由切割线定理得出(3+FG)2=BG×AG=2BG2,在Rt△BFG中,由勾股定理得:BG2=FG2﹣BF2推出FG2﹣6FG﹣27=0,求出FG即可,再在Rt△ABF中利用勾股定理即可解决问题.
(1)证明:连接OC,BC,
∵BD切⊙O于B,CH⊥AB,
∴∠CHA=∠DBA=90°,
∴CH∥BD,
∴△AEC∽△AFD,△AHE∽△ABF,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵CE=EH(E为CH中点),
∴BF=DF,
∵AB为⊙O的直径,
∴∠ACB=∠DCB=90°,
∵BF=DF,
∴CF=DF=BF(直角三角形斜边上的中线等于斜边的一半),
即CF=BF;

(2)证明:∵BF切⊙O于B,
∴∠DBA=90°,
∴∠DBC+∠CBA=90°,
∵AB为直径,
∴∠ACB=∠BCD=90°,
∴∠FBC=∠CAB,
∵OC=OA,CF=BF,
∴∠FCB=∠FBC,∠OCA=∠OAC,
∴∠FCB=∠CAB,
∵∠ACB=90°,
∴∠ACO+∠BCO=90°,
∴∠FCB+∠BCO=90°,
即OC⊥CF,
∴CF是⊙O切线;
(3)解:分别延长CF和AB交于点G,
∵BF=CF=DF(已证),FE=FB=3,
∴EF=FC=3,
∴∠FCE=∠FEC,
∵∠AHE=∠CHB=90°,
∴∠FAH+∠AEH=90°,∠G+∠GCH=90°,
∵∠AEH=∠CEF,
∴∠G=∠FAG,
∴AF=FG,
∵FB⊥AG,
∴AB=BG,
∵GBA是⊙O割线,AB=BG,FB=FE=3,
∴由切割线定理得:(3+FG)2=BG×AG=2BG2,
在Rt△BFG中,由勾股定理得:BG2=FG2﹣BF2,
∴FG2﹣6FG﹣27=0,
解得:FG=9或FG=﹣3(舍去),
∴AB=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
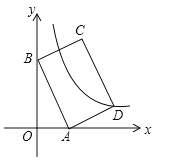
【题目】如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数![]() (x>0)的图像经过点D,则
(x>0)的图像经过点D,则![]() 值为( )
值为( )
A. ﹣14 B. 14 C. 7 D. ﹣7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济快速发展,环境问题越来越受到人们的关注.某校为了了解节能减排、垃圾分类等知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将结果绘制成以下两幅不完整的统计图,请根据统计图回答下列问题:
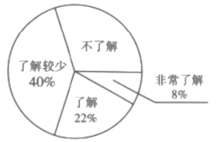
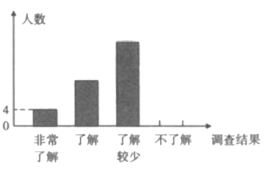
(1)本次调查的学生共有___________人,估计该校![]() 名学生中“不了解”的人数是__________人;
名学生中“不了解”的人数是__________人;
(2)将条形统计图补充完整;
(3)“非常了解”的![]() 人中有
人中有![]() ,
,![]() 两名男生,
两名男生,![]() ,
,![]() 两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图或列表的方法,求恰好抽到
两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图或列表的方法,求恰好抽到![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P和点![]() 关于x轴对称,点
关于x轴对称,点![]() 和点
和点![]() 关于直线l对称,则称点
关于直线l对称,则称点![]() 是点P关于x轴,直线l的二次对称点.
是点P关于x轴,直线l的二次对称点.
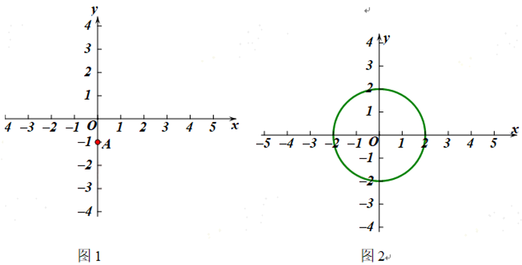
(1)如图1,点A(0,-1).
①若点B是点A关于x轴,直线![]() :x=2的二次对称点,则点B的坐标为 ;
:x=2的二次对称点,则点B的坐标为 ;
②点C (-4,1)是点A关于x轴,直线![]() :x=a的二次对称点,则a的值为 ;
:x=a的二次对称点,则a的值为 ;
③点D(-1,0)是点A关于x轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为 ;
的表达式为 ;
(2)如图2,O的半径为2.若O上存在点M,使得点M′是点M关于x轴,直线![]() :x = b的二次对称点,且点M′在射线
:x = b的二次对称点,且点M′在射线![]() (x≥0)上,b的取值范围是 ;
(x≥0)上,b的取值范围是 ;
(3)E(0,t)是y轴上的动点,E的半径为2,若E上存在点N,使得点N′是点N关于x轴,直线![]() :
:![]() 的二次对称点,且点N′在x轴上,求t的取值范围.
的二次对称点,且点N′在x轴上,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 上一点,经过点
上一点,经过点![]() ,
,![]() 的
的![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
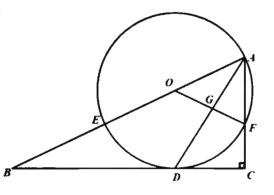
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)设![]() ,
,![]() ,试用含
,试用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
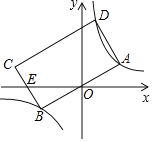
【题目】如图,矩形ABCD的顶点A,B,D分别落在双曲线y=![]() (k>0)的两个分支上,AB边经过原点O,CB边与x轴交于点E,且EC=EB,若点A的横坐标为1,则矩形ABCD的面积_____.
(k>0)的两个分支上,AB边经过原点O,CB边与x轴交于点E,且EC=EB,若点A的横坐标为1,则矩形ABCD的面积_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生睡眠时间的情况,随机调查了该校八年级 50 名学生,得到了一天睡眠时间的一组样本数据,如下:
睡眠时间 | 组中值 | 频数 |
|
| 3 |
| 6 | 3 |
| 7 |
|
| 8 | 25 |
| 9 | 10 |
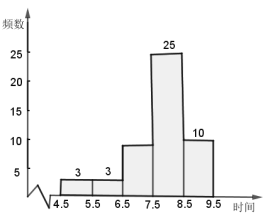
根据以上统计图表完成下列问题:
(1)统计表中![]() ;
;![]() ;
;
(2)根据数据,估算该校八年级学生平均每天睡眠时间;
(3)睡眠时间为 4.5~5.5h 的 3 名同学中有 1 名男生和 2 名女生,现从中随机挑选 2 名同学去医院进行健康体检,请用树状图法或列表法求出恰好选中“1 男 1 女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠BAC=90°,AB=AC=4,点D为BC上一点,点E为△ABC外一点,CE⊥AD,垂足为H,EB⊥BC,BF=EF,∠ADB+∠BDF=135°,则FD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,![]() 是
是![]() 上一动点,
上一动点,![]() 是
是![]() 外一点,在图中作出
外一点,在图中作出![]() 最小时的点
最小时的点![]() .
.
(2)如图2,![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心的
为圆心的![]() 的半径是
的半径是![]() ,
,![]() 是
是![]() 上一动点,在线段
上一动点,在线段![]() 上确定点
上确定点![]() 的位置,使
的位置,使![]() 的长最小,并求出其最小值.
的长最小,并求出其最小值.
(3)如图3,矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,
,![]() 为
为![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为直角边作
为直角边作![]() ,
,![]() ,
,![]() ,试探究四边形
,试探究四边形![]() 的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
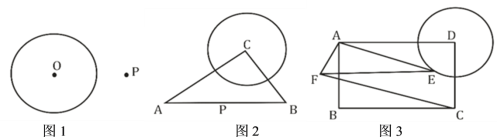
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com