
【题目】如图,Rt△ABC中,∠BAC=90°,AB=AC=4,点D为BC上一点,点E为△ABC外一点,CE⊥AD,垂足为H,EB⊥BC,BF=EF,∠ADB+∠BDF=135°,则FD的长为_____.

【答案】![]() .
.
【解析】
如图,取BC的中点O,连接OA,OF,在BO上取点G,使得BG=BF,则△BFG是等腰直角三角形.证明△AOD≌△OBF(ASA),推出OD=BF,设EF=BF=OD=a,则BG=a,FG=![]() a,OG=2
a,OG=2![]() ﹣a,DG=2
﹣a,DG=2![]() ﹣2a,再证明△FGO∽△DGF,推出
﹣2a,再证明△FGO∽△DGF,推出![]() =
=![]() ,由此构建方程求出a即可解决问题.
,由此构建方程求出a即可解决问题.
解:如图,取BC的中点O,连接OA,OF,在BO上取点G,使得BG=BF,则△BFG是等腰直角三角形.

∵AB=BC,∠BAC=90°,AO平分BC,
∴AO⊥BC,AO=BO=OC,
∴∠DAO+∠ADO=90°,
∵CH⊥AD,
∴∠DCH+∠ADO=90°,
∴∠DAO=∠DCH,
∵BO=OC,BF=EF,
∴OF∥CE,
∴∠FOB=∠DCH=∠DAO,
∴△AOD≌△OBF(ASA),
∴OD=BF,
设EF=BF=OD=a,则BG=a,FG=![]() a,OG=2
a,OG=2![]() ﹣a,DG=2
﹣a,DG=2![]() ﹣2a,
﹣2a,
∵∠ADB+∠BAD=180°﹣∠ABD=135°,且∠ADB+∠BDF=135°,
∴∠BDF=∠BAD,
∵∠DAO+∠BAD=45°,∠BDF+∠GFD=∠FGB=45°,
∴∠DAO=∠GFD,
∵∠FOB=∠DAO,
∴∠FOB=∠GFD,
∴△FGO∽△DGF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得a=![]() ,
,
∴BD=2![]() ﹣a=
﹣a=![]() ,
,
∴DF=![]() =
=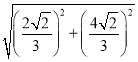 =
=![]() .
.
故答案为![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】对于平面内![]() 和
和![]() 外一点
外一点![]() ,若过点
,若过点![]() 的直线
的直线![]() 与
与![]() 有两个不同的公共点
有两个不同的公共点![]() ,点
,点![]() 为直线
为直线![]() 上的另一点,且满足
上的另一点,且满足![]() (如图1所示),则称点
(如图1所示),则称点![]() 是点
是点![]() 关于
关于![]() 的密切点.
的密切点.
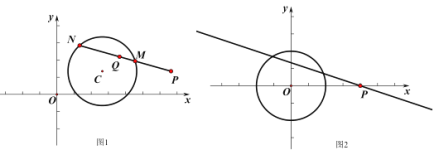
已知在平面直角坐标系![]() 中,
中, ![]() 的半径为2,点
的半径为2,点![]() .
.
(1)在点![]()
![]() 中,是点
中,是点![]() 关于
关于![]() 的密切点的为__________.
的密切点的为__________.
(2)设直线![]() 方程为
方程为![]() ,如图2所示,
,如图2所示,
①![]() 时,求出点
时,求出点![]() 关于
关于![]() 的密切点
的密切点![]() 的坐标;
的坐标;
②![]() 的圆心为
的圆心为![]() ,半径为2,若
,半径为2,若![]() 上存在点
上存在点![]() 关于
关于![]() 的密切点,直接写出
的密切点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
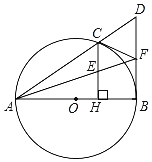
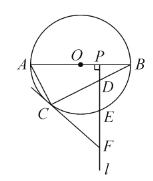
【题目】如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,连接CF.
(1)求证:CF=BF;
(2)求证:CF是⊙O的切线;
(3)若FB=FE=3,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年4月23日是世界读书日,某校为了解学生课外阅读情况,随机抽取20名学生,对每人每周用于课外阅读的平均时间(单位:min)进行调查,过程如下:
收集数据:
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:
课外阅读平均时间x(min) | 0≤x<40 | 40≤x<80 | 80≤x<120 | 120≤x<160 |
等级 | D | C | B | A |
人数 | 3 | a | 8 | b |
分析数据:
平均数 | 中位数 | 众数 |
80 | m | n |
请根据以上提供的信息,解答下列问题:
(1)填空:a= ,b= ;m= ,n= ;
(2)已知该校学生500人,若每人每周用于课外阅读的平均时间不少于80min为达标,请估计达标的学生数;
(3)设阅读一本课外书的平均时间为260min,请选择适当的统计量,估计该校学生每人一年(按52周计)平均阅读多少本课外书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°.
(1)尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母)
①作线段AC的垂直平分线l,交AC于点O;
②连接BO并延长,在BO的延长线上截取OD,使得OD=OB;
③连接DA、DC.
(2)判断四边形ABCD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是ABCD的AD边上一点,CE与BA的延长线交于点F,则下列比例式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中一定成立的是( )
,其中一定成立的是( )
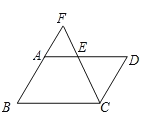
A.①③④B.①②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学学习小组“陆月辉煌”最近正在进行几何图形组合问题的研究.认真研读以下四个片段,并回答问题.
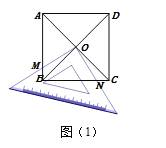
(片断一)小陆说:将一块足够大的等腰直角三角板置于一个正方形中,直角顶点与对角线交点O重合,在转动三角板的过程中我发现某些线段之间存在确定的数量关系.
如图(1),若三角板两条直角边的外沿分别交正方形的边AB、BC于点M、N,则①OM+ON=MB+NB;②![]() .
.
请你判断他的猜想是否正确?并证明你认为正确的猜想.
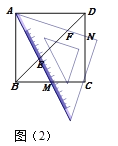
(片断二)小月说:将三角板中一个45°角的顶点和正方形的一个顶点重合放置,使得这个角的两条边与正方形的一组邻边有交点.
如图(2),若以A为顶点的45°角的两边分别交正方形的边BC、CD于点M、N,交对角线BD于点E、F.我发现:BE2+DE2=2AE2,只要准确旋转图(2)中的一个三角形就能证明这个结论.
请你写出小月所说的具体的旋转方式:______________________.
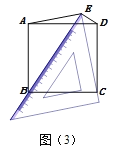
(片断三)小辉说:将三角板的一个45°角放置在正方形的外部,同时角的两边恰好经过正方形两个相邻的顶点.
如图(3),设顶点为E的45°角位于正方形的边AD上方,这个角的两边分别经过点B、C,连接EA,ED.那么线段EB、EC、ED也存在确定的数量关系:(EB+ED)2=2EC2.
请你证明这个结论.
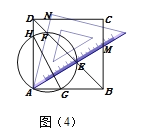
(片断四)小煌说:在图(2)中,作一个过点A、E、F的圆,交正方形的边AB、AD于点G、H,如图(4)所示.你知道线段DH、HG、GB三者之间的关系吗?请直接写出结论:________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是☉
是☉![]() 的直径,
的直径,![]() 为☉
为☉![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
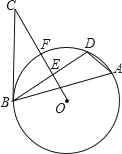
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com