
【题目】数学学习小组“陆月辉煌”最近正在进行几何图形组合问题的研究.认真研读以下四个片段,并回答问题.
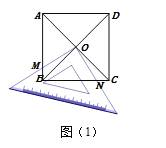
(片断一)小陆说:将一块足够大的等腰直角三角板置于一个正方形中,直角顶点与对角线交点O重合,在转动三角板的过程中我发现某些线段之间存在确定的数量关系.
如图(1),若三角板两条直角边的外沿分别交正方形的边AB、BC于点M、N,则①OM+ON=MB+NB;②![]() .
.
请你判断他的猜想是否正确?并证明你认为正确的猜想.
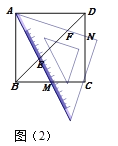
(片断二)小月说:将三角板中一个45°角的顶点和正方形的一个顶点重合放置,使得这个角的两条边与正方形的一组邻边有交点.
如图(2),若以A为顶点的45°角的两边分别交正方形的边BC、CD于点M、N,交对角线BD于点E、F.我发现:BE2+DE2=2AE2,只要准确旋转图(2)中的一个三角形就能证明这个结论.
请你写出小月所说的具体的旋转方式:______________________.
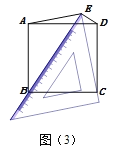
(片断三)小辉说:将三角板的一个45°角放置在正方形的外部,同时角的两边恰好经过正方形两个相邻的顶点.
如图(3),设顶点为E的45°角位于正方形的边AD上方,这个角的两边分别经过点B、C,连接EA,ED.那么线段EB、EC、ED也存在确定的数量关系:(EB+ED)2=2EC2.
请你证明这个结论.
(片断四)小煌说:在图(2)中,作一个过点A、E、F的圆,交正方形的边AB、AD于点G、H,如图(4)所示.你知道线段DH、HG、GB三者之间的关系吗?请直接写出结论:________________.
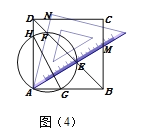
【答案】【片断一】①错误,②正确,证明见详解;【片断二】将△ABE绕点A逆时针旋转90°得到△ADG;【片断三】证明见详解;【片断四】DH+BG=GH.
【解析】
根据四边形ABCD是正方形,可以得出∠MOB=∠NOC,利用ASA可以证明△MOB≌△NOC,则可以判断②正确;作![]() 交BC于E点,根据等腰直角三角形的性质和垂线段最短可以判断①错误;
交BC于E点,根据等腰直角三角形的性质和垂线段最短可以判断①错误;
【片断二】将△ABE绕点A逆时针旋转90°得到△ADG.利用旋转的性质可以证明△AFG≌△AFE,则可判断△AGE是等腰直角三角形,利用勾股定理即可证明;
【片断三】过点C作EC的垂线交EB延长线于F,可证△FCE是等腰直角三角形,并可得△CDE≌△CBF,即可推出结论,解决问题;
【片断四】结论:DH+GB=HG.连接FH、CF、CE、EG,延长AB到J,使得BJ=DH,易证△ADF≌△CDF,利用三角形的内角和定理可以推出C、F、H共线,
同理也可得C、E、G共线,根据A、G、E、F、H共圆和圆周角的性质得到∠FCG=45°,可以推出∠BCJ +∠GBC=∠GCJ =45°=∠HCG,利用SAS可以证明△CGH≌△CGJ,则可以得到DH+BG=GH.
解:【片断一】:①错误,②正确;
理由:如图1中,作![]() 交BC于E点
交BC于E点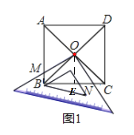
∵四边形ABCD是正方形,
∴AC⊥BD,OB=OC=OD=OA,∠ABO=∠OCN=45°,
∵∠MON=∠BOC=90°,
∴∠MON-∠BON =∠BOC-∠BON
∴∠MOB=∠NOC,
∴△MOB≌△NOC(ASA),
∴BM=CN,![]()
∴![]() ,
,
即②正确,
又∵![]() ,△BOC是等腰直角三角形,
,△BOC是等腰直角三角形,
则有![]() ,
,
∴![]()
即![]() ,故①错误;
,故①错误;
【片断二】
:将△ABE绕点A逆时针旋转90°得到△ADG; 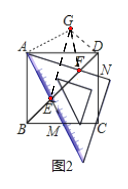
证明:如图2所示,连接GE,GF,
∵∠MAC=45°,并且由旋转可知∠BAE=∠DAG,AG=AE,
∴∠GAF=∠EAF=45°
又∵AF=AF,
∴△AFG≌△AFE(SAS),
∴GF=EF,∠GAF=∠EAF =45°,AG=AE,
∴∠GAF+∠EAF =90°,
即△AGE是等腰直角三角形,
∴![]() ,
,
又∵∠ADG=∠ABE=∠ADF=45°,
∴∠FDG=90°,
∴![]() ,
,
即有![]() .
.
故答案为:将△ABE绕点A逆时针旋转90°得到△ADG.
【片断三】:如图,过点C作EC的垂线交EB延长线于F,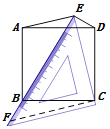
∵∠ECF=∠DCB=90°,
∴∠DCE=∠BCF,
∵∠BEC=45°,即△FCE是等腰直角三角形,
∴CE=CF,
∵CD=CB,
∴△CDE≌△CBF(SAS),
∴ED=FB,
∴EB+ED=EB+FB=EF,
又因为EC2+FC2=EF2,
∴(EB+ED)2=2EC2.
【片断四】:结论:DH+GB=HG.
证明:如图示,连接FH、CF、CE、EG,延长AB到J,使得BJ=DH,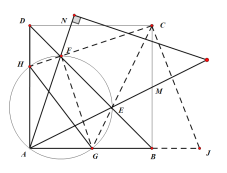
∵DC=DC,DF=DF,∠ADF=∠CDF=45°,
∴△ADF≌△CDF(SAS),
∴∠DAF=∠DCF,
由三角形的内角和定理可知:
∠DFC=180°-∠FDC-∠DCF =180°-45°-∠DCF=135°-∠DCF,
∠DFH=180°-∠FDH-∠DHF =180°-45°-∠DHF =135°-∠DHF,
∠DCF+∠DHF=90°,
∴∠DFH+∠DFC
=135°-∠DCF +135°-∠DHF
=270°-(∠DCF +∠DHF)
=270°-90°
=180°,
∴C、F、H共线,
同理可证C、E、G共线,
∵CD=CB,∠CDH=∠CBJ=90°,DH=BJ,
∴△CDH≌△CBJ(SAS),
∴CH=CJ,∠DCH=∠BCJ,
连接E,G,
∵A、G、E、F、H共圆,∠DAG=90°,
∴HG是圆的直径,
∴∠HFG=∠GFC=90°,并且∠FGE=∠FAE=45°,
∴∠FCG=45°,
∴∠DCH+∠GBC=45°,
即有∠BCJ +∠GBC=∠GCJ =45°=∠HCG,
在△CGH和△CGJ中

∴△CGH≌△CGJ(SAS),
∴HG=GJ,
∴DH+BG=GH.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】随着经济快速发展,环境问题越来越受到人们的关注.某校为了了解节能减排、垃圾分类等知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将结果绘制成以下两幅不完整的统计图,请根据统计图回答下列问题:
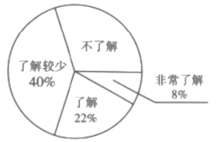
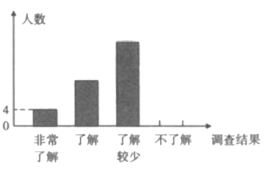
(1)本次调查的学生共有___________人,估计该校![]() 名学生中“不了解”的人数是__________人;
名学生中“不了解”的人数是__________人;
(2)将条形统计图补充完整;
(3)“非常了解”的![]() 人中有
人中有![]() ,
,![]() 两名男生,
两名男生,![]() ,
,![]() 两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图或列表的方法,求恰好抽到
两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图或列表的方法,求恰好抽到![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生睡眠时间的情况,随机调查了该校八年级 50 名学生,得到了一天睡眠时间的一组样本数据,如下:
睡眠时间 | 组中值 | 频数 |
|
| 3 |
| 6 | 3 |
| 7 |
|
| 8 | 25 |
| 9 | 10 |
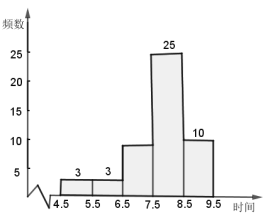
根据以上统计图表完成下列问题:
(1)统计表中![]() ;
;![]() ;
;
(2)根据数据,估算该校八年级学生平均每天睡眠时间;
(3)睡眠时间为 4.5~5.5h 的 3 名同学中有 1 名男生和 2 名女生,现从中随机挑选 2 名同学去医院进行健康体检,请用树状图法或列表法求出恰好选中“1 男 1 女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠BAC=90°,AB=AC=4,点D为BC上一点,点E为△ABC外一点,CE⊥AD,垂足为H,EB⊥BC,BF=EF,∠ADB+∠BDF=135°,则FD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以点M(0,![]() )为圆心,以
)为圆心,以![]() 长为半径作M交x轴于A.B两点,交y轴于C.D两点,连接AM并延长交M于P点,连接PC交x轴于E.
长为半径作M交x轴于A.B两点,交y轴于C.D两点,连接AM并延长交M于P点,连接PC交x轴于E.
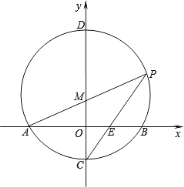
(1)求点C.P的坐标;
(2)求证:BE=2OE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情防控,我们一直在坚守.某居委会组织两个检查组,分别对“居民体温”和“居民安全出行”的情况进行抽查.若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查,则他们恰好抽到同一个小区的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
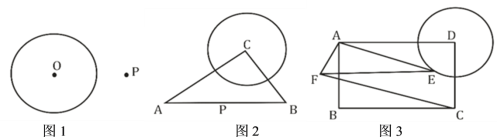
科目:初中数学 来源: 题型:
【题目】(1)如图1,![]() 是
是![]() 上一动点,
上一动点,![]() 是
是![]() 外一点,在图中作出
外一点,在图中作出![]() 最小时的点
最小时的点![]() .
.
(2)如图2,![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心的
为圆心的![]() 的半径是
的半径是![]() ,
,![]() 是
是![]() 上一动点,在线段
上一动点,在线段![]() 上确定点
上确定点![]() 的位置,使
的位置,使![]() 的长最小,并求出其最小值.
的长最小,并求出其最小值.
(3)如图3,矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,
,![]() 为
为![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为直角边作
为直角边作![]() ,
,![]() ,
,![]() ,试探究四边形
,试探究四边形![]() 的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直径,弦
为直径,弦![]() 交
交![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() ,
,![]() .
.
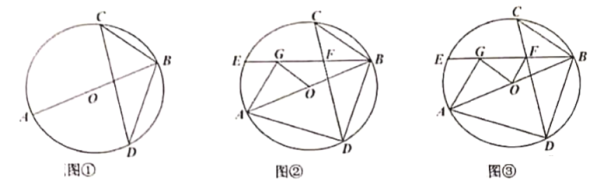
(1)如图①,求![]() 的度数;
的度数;
(2)如图②,弦![]() 交
交![]() 于点
于点![]() .在
.在![]() 上取点
上取点![]() ,连接
,连接![]() 、
、![]() 和
和![]() ,使
,使![]() ,求证:
,求证:![]() ;
;
(3)如图③,在(2)的条件下,![]() ,
,![]() 的直径为
的直径为![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com