练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．计算：（-$\frac{1}{3}$）-1-|-4|+$\sqrt{{3}^{2}+{4}^{2}}$+（sin30°）0．

    分析 本题涉及负整数指数幂、零指数幂、特殊角的三角函数值、二次根式化简四个考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．

    解答 解：（-$\frac{1}{3}$）-1-|-4|+$\sqrt{{3}^{2}+{4}^{2}}$+（sin30°）0
    =-3-4+5+1
    =-1．

    点评 本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟记特殊角的三角函数值，熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

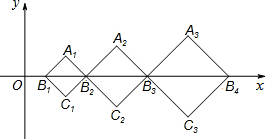    10．如图所示，在平面直角坐标系xOy中，B1（1，0），B2（3，0），B3（6，0），B4（10，0），…，以B1B2为对角线作第一个正方形A1B1C1B2，以B2B3为对角线作第二个正方形A2B2C2B3，以B3B4为对角线作第三个正方形A3B3C3B4，…，如果所作正方形的对角线BnBn+1的长度依次增加1个单位长度，顶点An都在第一象限内（n≥1，且n为整数），用n的代数式表示An的横坐标为$\frac{（π+1）^{2}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．2015年某省为加快建设综合交通体系，对铁路、公路、机场三个重大项目加大了建设资金的投入．

    （1）机场建设项目中所有6个机场投入的建设资金金额统计如图1，已知机场E投入的建设资金金额是机场C，D所投入建设资金金额之和的三分之二，求机场E投入的建设资金金额是多少亿元？并补全条形统计图；
    （2）将铁路、公路机场三项建设所投入的资金金额绘制成了如图2扇形统计图以及统计表，根据扇形统计图及统计表中信息，求得a=170，b=30，c60%，d122.4°，m=500．（请直接填写计算结果）
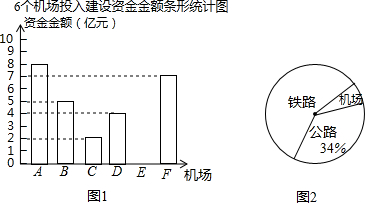
    铁路公路机场铁路、公路、机场三项投入建设资金总金额（亿元）
    投入资金（亿元）300abm
    所占百分比c34%6%
    所占圆心角216°d21.6°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．解不等式组$\left\{\begin{array}{l}{2x+5≥3}\\{3（x-2）＜2x-4}\end{array}\right.$，并把解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．为了帮扶本市一名特困儿童，某班有20名同学积极捐款，他们捐款的数额如下表：
    捐款的数额（单位：元）205080100
    人数（单位：名）6743
    对于这20名同学的捐款，众数是（　　）
    A．20元B．50元C．80元D．100元

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

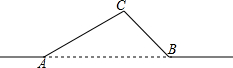    5．如图，一条输电线路从A地到B地需要经过C地，图中AC=20千米，∠CAB=30°，∠CBA=45°，因线路整改需要，将从A地到B地之间铺设一条笔直的输电线路．
    （1）求新铺设的输电线路AB的长度；（结果保留根号）
    （2）问整改后从A地到B地的输电线路比原来缩短了多少千米？（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．若关于x的分式方程$\frac{2}{x-3}$+$\frac{x+m}{3-x}$=2有增根，则m的值是（　　）
    A．m=-1B．m=0C．m=3D．m=0或m=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

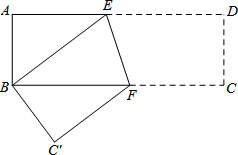    10．如图，在矩形纸片ABCD中，AB=4cm，AD=8cm，按如图方式折叠，使点D与点B重合，折痕为EF，则tan∠BEF=（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．设ω是一个平面图形，如果用直尺和圆规经过有限步作图（简称尺规作图），画出一个正方形与ω的面积相等（简称等积），那么这样的等积转化称为ω的“化方”．
    （1）阅读填空
    如图①，已知矩形ABCD，延长AD到E，使DE=DC，以AE为直径作半圆．延长CD交半圆于点H，以DH为边作正方形DFGH，则正方形DFGH与矩形ABCD等积．
    理由：连接AH，EH．
    ∵AE为直径，∴∠AHE=90°，∴∠HAE+∠HEA=90°．
    ∵DH⊥AE，∴∠ADH=∠EDH=90°
    ∴∠HAD+∠AHD=90°
    ∴∠AHD=∠HED，∴△ADH∽△HDE．
    ∴$\frac{AD}{DH}=\frac{DH}{DE}$，即DH2=AD×DE．
    又∵DE=DC
    ∴DH2=AD×DC，即正方形DFGH与矩形ABCD等积．
    （2）操作实践
    平行四边形的“化方”思路是，先把平行四边形转化为等积的矩形，再把矩形转化为等积的正方形．
    如图②，请用尺规作图作出与?ABCD等积的矩形（不要求写具体作法，保留作图痕迹）．
    （3）解决问题
    三角形的“化方”思路是：先把三角形转化为等积的矩形（填写图形名称），再转化为等积的正方形．
    如图③，△ABC的顶点在正方形网格的格点上，请作出与△ABC等积的正方形的一条边（不要求写具体作法，保留作图痕迹，不通过计算△ABC面积作图）．
    （4）拓展探究
    n边形（n＞3）的“化方”思路之一是：把n边形转化为等积的n-1边形，…，直至转化为等积的三角形，从而可以化方．
    如图④，四边形ABCD的顶点在正方形网格的格点上，请作出与四边形ABCD等积的三角形（不要求写具体作法，保留作图痕迹，不通过计算四边形ABCD面积作图）．

    查看答案和解析>>

    同步练习册答案