
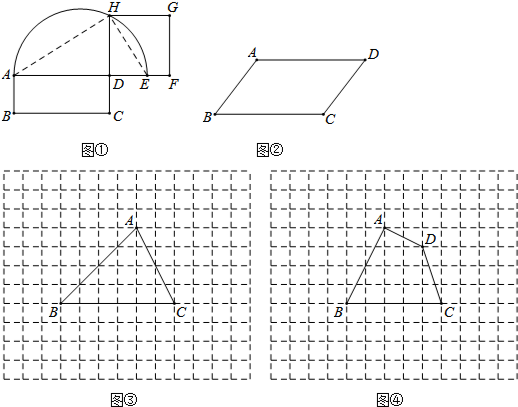
分析 (1)首先根据相似三角形的判定方法,可得△ADH∽△HDE;然后根据等量代换,可得DH2=AD×DC,据此判断即可.
(2)首先把平行四边形ABCD转化为等积的矩形ADMN,然后延长AD到E,使DE=DM,以AE为直径作半圆.延长MD交半圆于点H,以DH为边作正方形DFGH,则正方形DFGH与矩形ABMN等积,所以正方形DFGH与平行四边形ABCD等积,据此解答即可.
(3)首先以三角形的底为矩形的长,以三角形的高的一半为矩形的宽,将△ABC转化为等积的矩形MBCD;然后延长MD到E,使DE=DC,以ME为直径作半圆.延长CD交半圆于点H,则DH即为与△ABC等积的正方形的一条边.
(4)首先根据AG∥EH,判断出AG=2EH,然后根据CF=2DF,可得CF•EH=DF•AG,据此判断出S△CEF=S△ADF,S△CDI=S△AEI,所以S△BCE=S四边形ABCD,即△BCE与四边形ABCD等积,据此解答即可.
解答 解:(1)如图①,连接AH,EH,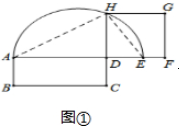
∵AE为直径,
∴∠AHE=90°,
∴∠HAE+∠HEA=90°.
∵DH⊥AE,
∴∠ADH=∠EDH=90°,
∴∠HAD+∠AHD=90°,
∴∠AHD=∠HED,
∴△ADH∽△HDE.
∴$\frac{AD}{DH}=\frac{DH}{DE}$,
即DH2=AD×DE.
又∵DE=DC,
∴DH2=AD×DC,
即正方形DFGH与矩形ABCD等积.
(2)作法:
①过A、D作AN、DM分别垂直BC于N、M;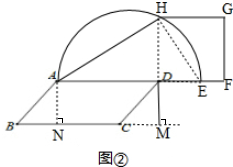
②延长AD,取DE=DM;
③以AE为直径作半圆O;
④延长MD交半圆O于H;
⑤以H、D作正方形HDFG,则正方形HDFG为平行四边形ABCD的等积正方形.
证明:
∵矩形ADMN的长和宽分别等于平行四边形ABCD的底和高,
∴矩形ADMN的面积等于平行四边形ABCD的面积,
∵AE为直径,
∴∠AHE=90°,
∴∠HAE+∠HEA=90°.
∵DH⊥AE,
∴∠ADH=∠EDH=90°,
∴∠HAD+∠AHD=90°,
∴∠AHD=∠HED,
∴△ADH∽△HDE.
∴$\frac{AD}{DH}=\frac{DH}{DE}$,
即DH2=AD×DE.
又∵DE=DM,
∴DH2=AD×DM,
即正方形DFGH与矩形ABMN等积,
∴正方形DFGH与平行四边形ABCD等积.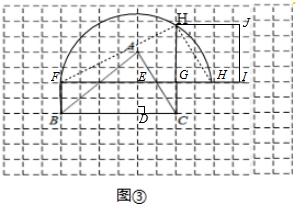
(3)作法:
①过A点作AD垂直BC于D;
②作AD的垂直平分线,取AD中点E;
③过E作BC平行线,作长方形BCGF,则S矩形BCGF=S△ABC;
其他步骤同(2)可作出其等积正方形.
(4)作法: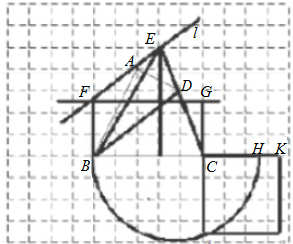
①过A点作BD平行线l;
②延长CD交平行线与E点;
③连接BE,则S四边形ABCD=S△EBC,
同(3)可作出其等积正方形.
△BCE与四边形ABCD等积,理由如下:
∵BD∥l,
∴S△ABD=S△EBD,
∴S△BCE=S四边形ABCD,
即△EBC与四边形ABCD等积.
故答案为:△HDE、AD×DC、矩形.
点评 (1)此题主要考查了相似形综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了矩形、三角形的面积的求法,以及对等积转化的理解,要熟练掌握.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:填空题
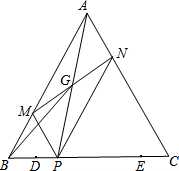 等边三角形ABC中,BC=6,D、E是边BC上两点,且BD=CE=1,点P是线段DE上的一个动点,过点P分别作AC、AB的平行线交AB、AC于点M、N,连接MN、AP交于点G,则点P由点D移动到点E的过程中,线段BG扫过的区域面积为$\frac{3\sqrt{3}}{2}$.
等边三角形ABC中,BC=6,D、E是边BC上两点,且BD=CE=1,点P是线段DE上的一个动点,过点P分别作AC、AB的平行线交AB、AC于点M、N,连接MN、AP交于点G,则点P由点D移动到点E的过程中,线段BG扫过的区域面积为$\frac{3\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
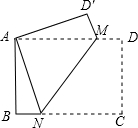 如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为( )
如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为( )| A. | 1:3 | B. | 1:4 | C. | 1:6 | D. | 1:9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
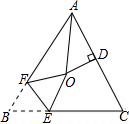 如图,△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AC的垂直平分线交于点O,将∠B沿EF(E在BC上,F在AB上)折叠,点B与点O恰好重合,则∠OEB为( )度.
如图,△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AC的垂直平分线交于点O,将∠B沿EF(E在BC上,F在AB上)折叠,点B与点O恰好重合,则∠OEB为( )度.| A. | 108 | B. | 120 | C. | 126 | D. | 128 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com