
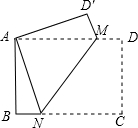
 如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为( )
如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为( )| A. | 1:3 | B. | 1:4 | C. | 1:6 | D. | 1:9 |
分析 由$\frac{BN}{CN}$=$\frac{1}{3}$,可知$\frac{BN}{AN}=\frac{1}{3}$,易证AN=AM,得到$\frac{BN}{AM}=\frac{1}{3}$,于是可求出△AMD′的面积与△AMN的面积的比.
解答 解:根据折叠的性质,AN=CN,∠ANM=∠CNM,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CNM=∠AMN,
∴∠ANM=∠AMN,
∴AM=AN,
∵$\frac{BN}{CN}$=$\frac{1}{3}$,
∴$\frac{BN}{AN}=\frac{1}{3}$,
∴$\frac{BN}{AM}=\frac{1}{3}$,
∴△AMD′的面积:△AMN的面积=1:3.
故选:A.
点评 本题主要考查了图形的折叠问题、等高的三角形面积比等于底的比,把△AMD′的面积与△AMN的面积的比转化为边的比,运用等高的三角形面积比等于底的比这一性质是解决问题的关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
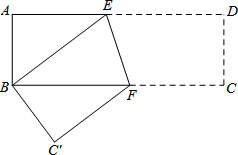 如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( )
如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
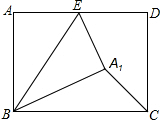 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )| A. | 3或4$\sqrt{2}$ | B. | 3$\sqrt{2}$或4$\sqrt{2}$ | C. | 3或4 | D. | 4或3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
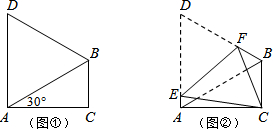
| A. | $\frac{\sqrt{3}-1}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{\sqrt{3}}{12}$ | D. | $\frac{\sqrt{3}-1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
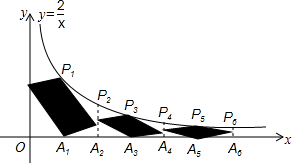 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上有点P1,P2,P3,…,它们的横坐标依次为1,2,3,…,分别过这些点作x轴的垂线,垂足依次为A1,A2,A3,…,分别以P1A1,P3A3,P5A5…为对角线作平行四边形,另两顶点分别落在P2n-2A2n-2与P2nA2n上(n=1,2,3,…,P0A0为y轴),所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,记P1=$\frac{1}{{S}_{1}}$,P2=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$,P3=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$,…,则P2=2;Pn-Pn-1=$\frac{2n-1}{2}$.
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上有点P1,P2,P3,…,它们的横坐标依次为1,2,3,…,分别过这些点作x轴的垂线,垂足依次为A1,A2,A3,…,分别以P1A1,P3A3,P5A5…为对角线作平行四边形,另两顶点分别落在P2n-2A2n-2与P2nA2n上(n=1,2,3,…,P0A0为y轴),所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,记P1=$\frac{1}{{S}_{1}}$,P2=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$,P3=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$,…,则P2=2;Pn-Pn-1=$\frac{2n-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
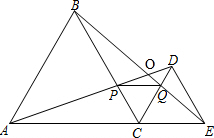 如图,C为线段AE上一动点(不与A,E重合),在AE同侧分别作等边△ABC和等边△ECD,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,则有以下五个结论:
如图,C为线段AE上一动点(不与A,E重合),在AE同侧分别作等边△ABC和等边△ECD,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,则有以下五个结论:| A. | ①③⑤ | B. | ①③④⑤ | C. | ①②③⑤ | D. | ①②③④⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com