
| A. | $\frac{\sqrt{3}-1}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{\sqrt{3}}{12}$ | D. | $\frac{\sqrt{3}-1}{6}$ |
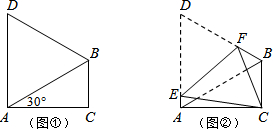
分析 在Rt△ABC中,设AB=2a,已知∠ACB=90°,∠CAB=30°,即可求得AB、AC的值,由折叠的性质知:DE=CE,可设出DE、CE的长,然后表示出AE的长,进而可在Rt△AEC中,由勾股定理求得AE、CE的值,即可求∠ACE的正弦值.
解答 解:∵△ABC中,∠ACB=90°,∠BAC=30°,设AB=2a,
∴AC=$\sqrt{3}$a,BC=a;
∵△ABD是等边三角形,
∴AD=AB=2a;
设DE=EC=x,则AE=2a-x;
在Rt△AEC中,由勾股定理,得:(2a-x)2+3a2=x2,解得x=$\frac{7}{4}a$;
∴AE=$\frac{1}{4}a$,EC=$\frac{7}{4}a$,
∴sin∠ACE=$\frac{AE}{CE}$=$\frac{1}{7}$.
故选:B.
点评 本题考查的是翻折变换,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 156 | B. | 162 | C. | 165 | D. | 167 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
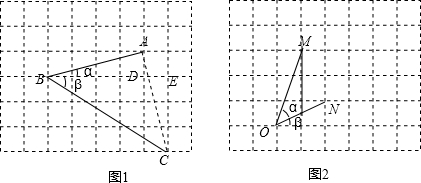
 (1)O是正△ABC的中心,它是△ABC的外接圆与内切圆的圆心.
(1)O是正△ABC的中心,它是△ABC的外接圆与内切圆的圆心.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
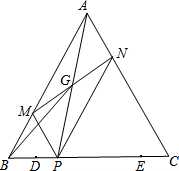 等边三角形ABC中,BC=6,D、E是边BC上两点,且BD=CE=1,点P是线段DE上的一个动点,过点P分别作AC、AB的平行线交AB、AC于点M、N,连接MN、AP交于点G,则点P由点D移动到点E的过程中,线段BG扫过的区域面积为$\frac{3\sqrt{3}}{2}$.
等边三角形ABC中,BC=6,D、E是边BC上两点,且BD=CE=1,点P是线段DE上的一个动点,过点P分别作AC、AB的平行线交AB、AC于点M、N,连接MN、AP交于点G,则点P由点D移动到点E的过程中,线段BG扫过的区域面积为$\frac{3\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
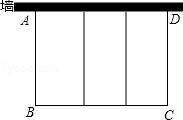 如图,孔明想利用一面长为45米的墙建羊圈,用100米的围栏围成总面积为600平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?孔明能在原来的基础上建一个面积为640平方米的羊圈吗?说说理由.
如图,孔明想利用一面长为45米的墙建羊圈,用100米的围栏围成总面积为600平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?孔明能在原来的基础上建一个面积为640平方米的羊圈吗?说说理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
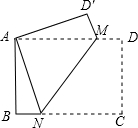 如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为( )
如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为( )| A. | 1:3 | B. | 1:4 | C. | 1:6 | D. | 1:9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
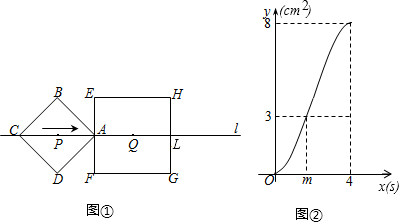
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com