
 (1)O是正△ABC的中心,它是△ABC的外接圆与内切圆的圆心.
(1)O是正△ABC的中心,它是△ABC的外接圆与内切圆的圆心.分析 (1)根据正多边形中心的定义及正三角形的性质即可求解;
(2)根据正多边形半径的定义及正三角形的性质即可求解;
(3)根据正多边形边心距的定义及正三角形的性质即可求解;
(4)根据正多边形中心角的定义及正三角形的性质即可求解.
解答 解:(1)O是正△ABC的中心,它是△ABC的外接圆与内切圆的圆心.
(2)OB叫正△ABC的半径,它是正△ABC的外接圆的半径.
(3)OD叫作正△ABC的边心距,它是正△ABC的内切圆的半径.
(4)∠BOC是正△ABC的中心角;∠BOC=120度;∠BOD=60度.
故答案为中心,外接,内切;半径,外接;边心距,内切;中心角,120,60.
点评 本题考查了正多边形与圆的关系及正多边形的有关概念.
①中心:正多边形的外接圆的圆心叫做正多边形的中心.
②正多边形的半径:外接圆的半径叫做正多边形的半径.
③中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.
④边心距:中心到正多边形的一边的距离叫做正多边形的边心距.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| 捐款的数额(单位:元) | 20 | 50 | 80 | 100 |
| 人数(单位:名) | 6 | 7 | 4 | 3 |
| A. | 20元 | B. | 50元 | C. | 80元 | D. | 100元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=-1 | B. | m=0 | C. | m=3 | D. | m=0或m=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
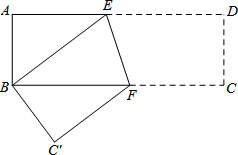 如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( )
如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
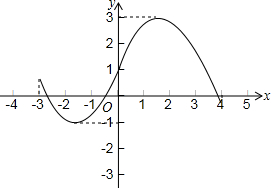 若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.
若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
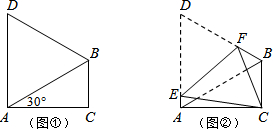
| A. | $\frac{\sqrt{3}-1}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{\sqrt{3}}{12}$ | D. | $\frac{\sqrt{3}-1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com