
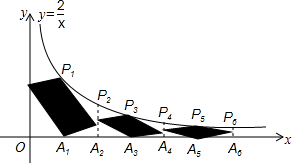
 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上有点P1,P2,P3,…,它们的横坐标依次为1,2,3,…,分别过这些点作x轴的垂线,垂足依次为A1,A2,A3,…,分别以P1A1,P3A3,P5A5…为对角线作平行四边形,另两顶点分别落在P2n-2A2n-2与P2nA2n上(n=1,2,3,…,P0A0为y轴),所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,记P1=$\frac{1}{{S}_{1}}$,P2=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$,P3=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$,…,则P2=2;Pn-Pn-1=$\frac{2n-1}{2}$.
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上有点P1,P2,P3,…,它们的横坐标依次为1,2,3,…,分别过这些点作x轴的垂线,垂足依次为A1,A2,A3,…,分别以P1A1,P3A3,P5A5…为对角线作平行四边形,另两顶点分别落在P2n-2A2n-2与P2nA2n上(n=1,2,3,…,P0A0为y轴),所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,记P1=$\frac{1}{{S}_{1}}$,P2=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$,P3=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$,…,则P2=2;Pn-Pn-1=$\frac{2n-1}{2}$. 分析 根据反比例函数图象上点的坐标特征得到P1(1,2),P3(3,$\frac{3}{2}$),P5(5,$\frac{2}{5}$),…,P2n-1(2n-1,$\frac{2}{2n-1}$),再根据平行四边形的性质和三角形面积公式可计算出S1=2,S2=$\frac{2}{3}$,S3=$\frac{2}{5}$,Sn=$\frac{2}{2n-1}$,所以P1=$\frac{1}{2}$,P2=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$=2,由于Pn-Pn-1=$\frac{1}{{S}_{n}}$,然后把Sn=$\frac{2}{2n-1}$代入计算即可.
解答 解:∵反比例函数y=$\frac{2}{x}$(x>0)的图象上有点P1,P2,P3,…,它们的横坐标依次为1,2,3,…,
∴P1(1,2),P3(3,$\frac{2}{3}$),P5(5,$\frac{2}{5}$),…,P2n-1(2n-1,$\frac{2}{2n-1}$),
∴S1=2×$\frac{1}{2}$×1×2=2,S2=2×$\frac{1}{2}$×1×$\frac{2}{3}$=$\frac{2}{3}$,S3=2×$\frac{1}{2}$×1×$\frac{2}{5}$=$\frac{2}{5}$,Sn=2×$\frac{1}{2}$×1×$\frac{2}{2n-1}$=$\frac{2}{2n-1}$,
∴P1=$\frac{1}{{S}_{1}}$=$\frac{1}{2}$,
P2=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$=$\frac{1}{2}$+$\frac{3}{2}$=2,
Pn-Pn-1=$\frac{1}{{S}_{n}}$=$\frac{2n-1}{2}$.
故答案为2,$\frac{2n-1}{2}$.
点评 本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.也考查了三角形面积公式和反比例函数图象上点的坐标特征.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
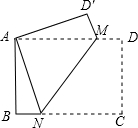 如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为( )
如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为( )| A. | 1:3 | B. | 1:4 | C. | 1:6 | D. | 1:9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
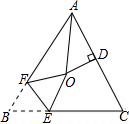 如图,△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AC的垂直平分线交于点O,将∠B沿EF(E在BC上,F在AB上)折叠,点B与点O恰好重合,则∠OEB为( )度.
如图,△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AC的垂直平分线交于点O,将∠B沿EF(E在BC上,F在AB上)折叠,点B与点O恰好重合,则∠OEB为( )度.| A. | 108 | B. | 120 | C. | 126 | D. | 128 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-8)-8=0 | B. | 3+$\sqrt{3}$=3$\sqrt{3}$ | C. | (-3b)2=9b2 | D. | a6÷a2=a3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,0) | B. | (-1,-2) | C. | (-1,2) | D. | (3,-4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com