【题目】某校计划购买一批排球和足球，已知购买2个排球和1个足球共需321元，购买3个排球和2个足球共需540元.
(1)求每个排球和足球的售价；
(2)若学校计划购买这两种球共50个，总费用不超过5500元，那么最多可购买足球多少个？
口算题卡北京妇女儿童出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，在等腰直角三角形ACD，∠ACD=90°，AC=
，分别以边AD，AC，CD为直径面半图，所得两个月形图案AGCE和DHCF的面积之和(图中阴影部分)为_____________。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，点
为直线
上一点，过点作射线
，使
，将一直角三角板的直角顶点放在点处，一边
在射线
上，另一边
在直线的上方.
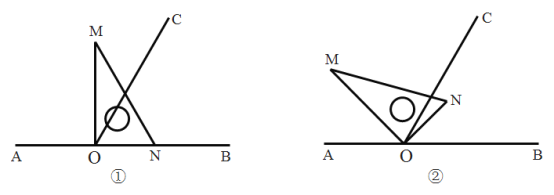
（1）在图①中，
__________度；
（2）将图①中的三角板绕点按逆时针方向旋转，使得在
的内部，如图②，若
，求
的度数；
（3）将图①中的三角板绕点以每秒
的速度沿逆时针方向旋转一周，在旋转的过程中，当直线恰好平分锐角时，旋转的时间是__________秒.（直接写出结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将n个边长都为2的正方形按如图所示摆放，点A1，A2，…An分别是正方形的中心，则这n个正方形重叠部分的面积之和是（ ）
A.nB.n﹣1C.
D.
n
查看答案和解析>>
科目：初中数学 来源： 题型：
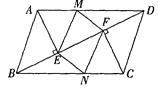
【题目】如图，已知四边形ABCD为平行四边形，AE⊥BD于E，CF⊥BD于F．
（1）求证：BE＝DF；
（2）若M、N分别为边AD、BC上的点，且DM=BN，试猜想四边形MENF的形状，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
经过点
，
，与
轴正半轴交于
点，与
轴交于
点.
(1)求直线
的解析式；
(2)设点
为直线下方抛物线上一点，连接
、
，当
面积最大时，求点的坐标；
(3)在(2)的条件下，直线
过直线与轴的交点
.设
的中点为
，
是直线上一点，
是直线上一点，求
周长的最小值.
查看答案和解析>>
科目：初中数学 来源： 题型：
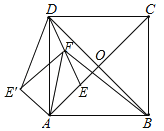
【题目】如图，正方形ABCD中，对角线AC、BD相交于点O，DE平分∠ADO交AC于点E，把△ADE沿AD翻折，得到△ADE′，点F是DE的中点，连接AF、BF、E′F．若AE＝2
．则四边形ABFE′的面积是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某核桃种植基地计划种植A、B两种优质核桃共30亩，已知这两种核桃的年产量分别为800千克/亩、1000千克/亩，收购价格分别是4.2元/千克、4元/千克．
(1)若该基地收获两种核桃的年总产量为25800千克，则A、B两种核桃各种植了多少亩？
(2)设该基地种植A种核桃a亩，全部收购后，总收入为w元，求出w与a之间的函数关系式．若要求种植A种核桃的面积不少于B种核桃的一半，那么种植A、B两种核桃各多少亩时，该种植基地的总收入最多？最多是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】今年九江正在创建“全国文明城市”，小华就公众对在餐厅吸烟的态度进行了随机抽样调查，主要有四种态度：A. 顾客出面制止；B. 劝说进吸烟室；C. 餐厅老板出面制止；D. 无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题：
（1）这次抽样的公众有______人；
（2）请将统计图①补充完整；
（3）在统计图②中，求出“无所谓”部分所对应的圆心角的度数；
（4）若城区人口有20万人，估计赞成“餐厅老板出面制止”的有多少万人？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
