
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,与
,与![]() 轴正半轴交于
轴正半轴交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 点.
点.
(1)求直线![]() 的解析式;
的解析式;
(2)设点![]() 为直线
为直线![]() 下方抛物线上一点,连接
下方抛物线上一点,连接![]() 、
、![]() ,当
,当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,直线![]() 过直线
过直线![]() 与
与![]() 轴的交点
轴的交点![]() .设
.设![]() 的中点为
的中点为![]() ,
,![]() 是直线
是直线![]() 上一点,
上一点,![]() 是直线
是直线![]() 上一点,求
上一点,求![]() 周长的最小值.
周长的最小值.

【答案】(1)y=2x-3(2)当![]() 时,
时,![]() 有最大值,此时P(2,-3)(3)
有最大值,此时P(2,-3)(3)![]()
【解析】分析:(1)把点A的坐标代入![]() 中求出二次函数的解析式,得点C的坐标,用待定系数法求AC的解析式;(2)设
中求出二次函数的解析式,得点C的坐标,用待定系数法求AC的解析式;(2)设![]() ,则过P作
,则过P作![]() 轴的平行线与AC的交点坐标为
轴的平行线与AC的交点坐标为![]() ,用含x的式子表示出
,用含x的式子表示出![]() ,结合二次函数的性质求解;(3)判断点F关于CP的对称点Q的坐标,关于直线
,结合二次函数的性质求解;(3)判断点F关于CP的对称点Q的坐标,关于直线![]() 的对称点是原点O,则△EHF的周长的最小值是OQ的长.
的对称点是原点O,则△EHF的周长的最小值是OQ的长.
详解:(1)…![]()
(2)设![]() ,则过P作
,则过P作![]() 轴的平行线与AC的交点坐标为
轴的平行线与AC的交点坐标为![]() ,
,
![]()
![]() .
.
所以当x=2时,![]() 有最大值,此时P(2,-3)
有最大值,此时P(2,-3)
(3)B(3,0),C(0,-3),则![]() ,F关于PC的对称点为
,F关于PC的对称点为![]()
直线![]() 过D(
过D(![]() ,0),所以直线
,0),所以直线![]() 的解析式为
的解析式为![]() ,
,
所以F点关于直线![]() 的对称点为原点,
的对称点为原点,
所以△EHF的周长的最小值为OQ的长,
根据勾股定理得,OQ=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是全面调查 B. 样本容量是360
C. 该校只有360个家长持反对态度 D. 该校约有90%的家长持反对态度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?
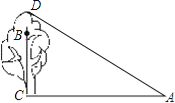
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批排球和足球,已知购买2个排球和1个足球共需321元,购买3个排球和2个足球共需540元.
(1)求每个排球和足球的售价;
(2)若学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买足球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面内有不共线的3个点,![]() ,
,![]() ,
,![]() .
.
(1)作射线![]() ,在
,在![]() 延长线上取一点
延长线上取一点![]() ,使
,使![]() ;
;
(2)作线段![]() 并延长
并延长![]() 到点
到点![]() ,使
,使![]() ;
;
(3)连接![]() ,
,![]() ;
;
(4)度量线段![]() 和
和![]() 的长度,直接写出二者之间的数量关系,观察
的长度,直接写出二者之间的数量关系,观察![]() 和
和![]() 的位置是(填“平行”或“相交”)关系;
的位置是(填“平行”或“相交”)关系;
(5)作![]() 的中点
的中点![]() ,连接
,连接![]() ,猜想
,猜想![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上,点![]() 和点
和点![]() 分别位于原点
分别位于原点![]() 两侧,点
两侧,点![]() 对应的数为
对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,且
,且![]() .
.
(1)若![]() ,则
,则![]() 的值为.
的值为.
(2)若![]() ,求
,求![]() 的值;
的值;
(3)点![]() 为数轴上一点,对应的数为
为数轴上一点,对应的数为![]() ,若
,若![]() 点在原点的左侧,
点在原点的左侧,![]() 为
为![]() 的中点,
的中点,![]() ,请画出图形并求出满足条件的
,请画出图形并求出满足条件的![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】季末打折促销,甲乙两商场促销方式不同,两商场实际付费![]() (元)与标价
(元)与标价![]() (元)之间的函数关系如图所示折线
(元)之间的函数关系如图所示折线![]() (虚线)表示甲商场,折线
(虚线)表示甲商场,折线![]() 表示乙商场
表示乙商场
(1)分别求射线![]() 的解析式.
的解析式.
(2)张华说他必须选择乙商场,由此推理张华计划购物所需费用![]() (元)(标价)的范围是______.
(元)(标价)的范围是______.
(3)李明说他必须选择甲商场,由此推理李明计划购物所需费用![]() (元)(标价)的范围是______.
(元)(标价)的范围是______.
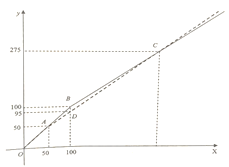
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com