
【题目】已知数轴上,点![]() 和点
和点![]() 分别位于原点
分别位于原点![]() 两侧,点
两侧,点![]() 对应的数为
对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,且
,且![]() .
.
(1)若![]() ,则
,则![]() 的值为.
的值为.
(2)若![]() ,求
,求![]() 的值;
的值;
(3)点![]() 为数轴上一点,对应的数为
为数轴上一点,对应的数为![]() ,若
,若![]() 点在原点的左侧,
点在原点的左侧,![]() 为
为![]() 的中点,
的中点,![]() ,请画出图形并求出满足条件的
,请画出图形并求出满足条件的![]() 的值.
的值.

科目:初中数学 来源: 题型:
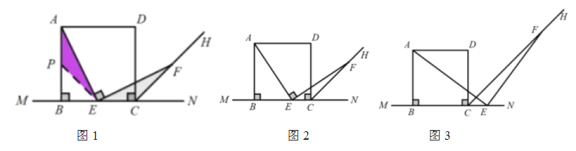
【题目】如图1,以直线MN上的线段BC为边作正方形ABCD,CH平分∠DCN,点E为射线BN上一点,连接AE,过点E作AE的垂线交射线CH于点F,探索AE与EF的数量关系。
(1)阅读下面的解答过程。并按此思路完成余下的证明过程
当点E在线段BC上,且点E为BC中点时,AB=EF
理由如下:
取AB中点P,達接PE
在正方形ABCD中,∠B=∠BCD=90°,AB=BC
∴△BPE等腰三角形,AP=BC
∴∠BPB=45°
∴∠APBE=135°
又因为CH平分∠DCN
∴∠DCF=45°
∴∠ECF=135°
∴∠APE=∠ECF
余下正明过程是:
(2)当点E为线段AB上任意一点时,如图2,结论“AE=EF”是否成立,如果成立,请给出证明过程;
(3)当点E在BC的延长线时,如图3,结论“AE=EF”是否仍然成立,如果成立,请在图3中画出必要的辅助线(不必说明理由)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )

A.nB.n﹣1C.![]() D.
D.![]() n
n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,与
,与![]() 轴正半轴交于
轴正半轴交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 点.
点.
(1)求直线![]() 的解析式;
的解析式;
(2)设点![]() 为直线
为直线![]() 下方抛物线上一点,连接
下方抛物线上一点,连接![]() 、
、![]() ,当
,当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,直线![]() 过直线
过直线![]() 与
与![]() 轴的交点
轴的交点![]() .设
.设![]() 的中点为
的中点为![]() ,
,![]() 是直线
是直线![]() 上一点,
上一点,![]() 是直线
是直线![]() 上一点,求
上一点,求![]() 周长的最小值.
周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
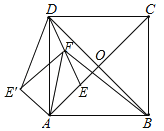
【题目】如图,正方形ABCD中,对角线AC、BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF、BF、E′F.若AE=2![]() .则四边形ABFE′的面积是_____.
.则四边形ABFE′的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某核桃种植基地计划种植A、B两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.
(1)若该基地收获两种核桃的年总产量为25800千克,则A、B两种核桃各种植了多少亩?
(2)设该基地种植A种核桃a亩,全部收购后,总收入为w元,求出w与a之间的函数关系式.若要求种植A种核桃的面积不少于B种核桃的一半,那么种植A、B两种核桃各多少亩时,该种植基地的总收入最多?最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学活动课中,小敏为了测量校园内旗杆![]() 的高度.先在教学楼的底端
的高度.先在教学楼的底端![]() 点处,观测到旗杆顶端
点处,观测到旗杆顶端![]() 得
得![]() ,然后爬到教学楼上的
,然后爬到教学楼上的![]() 处,观测到旗杆底端
处,观测到旗杆底端![]() 的俯角是
的俯角是![]() .已知教学楼中
.已知教学楼中![]() 、
、![]() 两处高度为
两处高度为![]() 米.
米.
(1)求教学楼与旗杆的水平距离![]() ;(结果保留根号);
;(结果保留根号);
(2)求旗杆![]() 的高度.
的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位计划组织员工到 地旅游,人数估计在![]() 之间,甲乙两旅行社的服务质量相同,组织到
之间,甲乙两旅行社的服务质量相同,组织到![]() 地旅游的价格都是每人200元,在洽谈时,甲旅行社表示可给予每位旅客七五折(即原价格的75%)优惠;乙旅行社表示可先免去一位旅客的旅游费用,其余旅客八折优惠,该单位怎样选择,才能使其支付的旅游总费用较少?
地旅游的价格都是每人200元,在洽谈时,甲旅行社表示可给予每位旅客七五折(即原价格的75%)优惠;乙旅行社表示可先免去一位旅客的旅游费用,其余旅客八折优惠,该单位怎样选择,才能使其支付的旅游总费用较少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com