
 如图,梯形ABCD中,AD∥BC,DE∥AB交BC边于点E.那么下列事件中属于随机事件的是( )
如图,梯形ABCD中,AD∥BC,DE∥AB交BC边于点E.那么下列事件中属于随机事件的是( )| A. | $\overrightarrow{AD}$=$\overrightarrow{EB}$ | B. | $\overrightarrow{AB}$=$\overrightarrow{DC}$ | C. | $\overrightarrow{AB}$=$\overrightarrow{DE}$ | D. | $\overrightarrow{AD}$=$\overrightarrow{EC}$ |
分析 根据平行四边形的判定定理得到四边形ABED是平行四边形,根据向量的性质和随机事件的概念进行判断即可.
解答 解:∵AD∥BC,DE∥AB,
∴四边形ABED是平行四边形,
$\overrightarrow{AD}$=$\overrightarrow{EB}$是不可能事件;
$\overline{AB}$=$\overrightarrow{DC}$是不可能事件;
$\overrightarrow{AB}$=$\overrightarrow{DE}$是必然事件;
$\overrightarrow{AD}$=$\overrightarrow{EC}$是随机事件,
故选:D.
点评 本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:解答题
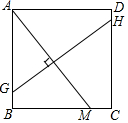 如图所示,在正方形ABCD中,M是BC上一点,连接AM,作AM垂直平分线GH交AB于G点,交CD于H点,已知AB=8,CM=2,求GH长.
如图所示,在正方形ABCD中,M是BC上一点,连接AM,作AM垂直平分线GH交AB于G点,交CD于H点,已知AB=8,CM=2,求GH长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
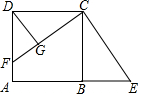 如图,正方形ABCD中,AB=20,F为AD上的点,连接CF,作CE⊥CF交AB的延长线于点E,作DG⊥CF于点G,若BE=15,CE=25,则DG的长度为12.
如图,正方形ABCD中,AB=20,F为AD上的点,连接CF,作CE⊥CF交AB的延长线于点E,作DG⊥CF于点G,若BE=15,CE=25,则DG的长度为12.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2$\sqrt{2}$ | C. | ±1 | D. | $±2\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 80° | B. | 20° | C. | 80°或20° | D. | 以上均不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com