
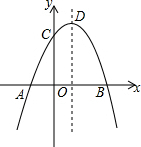
 ��ͼ��������y=-x2+2x+m+1��x���ڵ�A��a��0����B��b��0������y���ڵ�C�������ߵĶ���ΪD�������ĸ����⣺�ٵ�x��0ʱ��y��0�� ����a=-1����b=3������������������P��x1��y1����Q��x2��y2������x1��1��x2����x1+x2��2����y1��y2���ܵ�C���������߶Գ��� �ĶԳƵ�ΪE����G��F�ֱ���x���y���ϣ���m=2ʱ���ı���EDFG�ܳ�����СֵΪ6$\sqrt{2}$��������ȷ�������У�����������
��ͼ��������y=-x2+2x+m+1��x���ڵ�A��a��0����B��b��0������y���ڵ�C�������ߵĶ���ΪD�������ĸ����⣺�ٵ�x��0ʱ��y��0�� ����a=-1����b=3������������������P��x1��y1����Q��x2��y2������x1��1��x2����x1+x2��2����y1��y2���ܵ�C���������߶Գ��� �ĶԳƵ�ΪE����G��F�ֱ���x���y���ϣ���m=2ʱ���ı���EDFG�ܳ�����СֵΪ6$\sqrt{2}$��������ȷ�������У�����������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� �ٸ��ݶ��κ����������ޣ��жϳ�y�ķ��ţ�
�ڸ���A��B���ڶԳ���Գƣ����b��ֵ��
�۸���$\frac{{x}_{1}+{x}_{2}}{2}$��1���õ�x1��1��x2���Ӷ��õ�Q�����Գ����Զ�������жϳ�y1��y2��
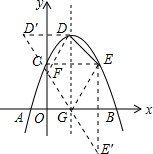
����D����y��ĶԳƵ�D�䣬E����x��ĶԳƵ�E�䣬����D��E�䣬D��E����DE�ĺͼ�Ϊ�ı���EDFG�ܳ�����Сֵ�����D��E��D�䡢E������꼴�ɽ��
��� �⣺�� ��x��0ʱ������ͼ���һ�����ޣ���0��x��bʱ��y��0����x��bʱ��y��0���ʱ�ѡ�����
��x��0ʱ������ͼ���һ�����ޣ���0��x��bʱ��y��0����x��bʱ��y��0���ʱ�ѡ�����
�ڶ��κ����Գ���Ϊx=-$\frac{2}{2����-1��}$=1����a=-1ʱ��$\frac{-1+b}{2}$=1�����b=3���ʱ�ѡ����ȷ��
�ۡ�x1+x2��2��
��$\frac{{x}_{1}+{x}_{2}}{2}$��1��
�֡�x1-1��1��x2-1��
��Q�����Գ����Զ��
��y1��y2���ʱ�ѡ����ȷ��
����ͼ����D����y��ĶԳƵ�D�䣬E����x��ĶԳƵ�E�䣬
����D��E�䣬D��E����DE�ĺͼ�Ϊ�ı���EDFG�ܳ�����Сֵ��
��m=2ʱ�����κ���Ϊy=-x2+2x+3������������Ϊy=-1+2+3=4��DΪ��1��4������D��Ϊ��-1��4����C������ΪC��0��3������EΪ��2��3����E��Ϊ��2��-3����
��DE=$\sqrt{��2-1��^{2}+��3-4��^{2}}$=$\sqrt{2}$��D��E��=$\sqrt{��-1-2��^{2}+��-3-4��^{2}}$=$\sqrt{58}$��
���ı���EDFG�ܳ�����СֵΪ$\sqrt{2}$+$\sqrt{58}$���ʱ�ѡ�����
��ȷ����2����
��ѡ��B��
���� ���⿼���˶��κ����ۺ��⣬�漰�����벻��ʽ�Ĺ�ϵ�����κ����ĶԳ��ᡢ����ͼ���ϵ��������������Գ�--���·������ȣ����ն��κ��������ʣ���ԳƵ������ǽ������Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
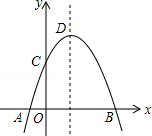 ��ͼ��������y=-x2+2x+m+1��x���ڵ�A��a��0����B��b��0������y���ڵ�C�������ߵĶ���ΪD�������ĸ����⣺
��ͼ��������y=-x2+2x+m+1��x���ڵ�A��a��0����B��b��0������y���ڵ�C�������ߵĶ���ΪD�������ĸ����⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
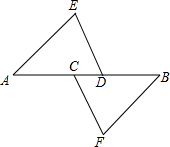 ��֪����ͼ��C��D��AB�ϣ���AC=BD��AE��FB��DE��FC����֤��AE=BF��
��֪����ͼ��C��D��AB�ϣ���AC=BD��AE��FB��DE��FC����֤��AE=BF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
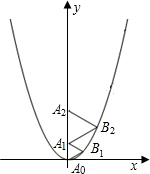 ���κ���y=$\frac{2}{3}$x2��ͼ����ͼ��ʾ����A0λ������ԭ�㣬�� A1��A2��y����������ϣ���B1��B2�ڶ��κ���y=$\frac{2}{3}$x2λ�ڵ�һ����ͼ���ϣ�����A0B1A1����A1B2A2��Ϊ�ȱ������Σ����A1B2A2�ı߳���������
���κ���y=$\frac{2}{3}$x2��ͼ����ͼ��ʾ����A0λ������ԭ�㣬�� A1��A2��y����������ϣ���B1��B2�ڶ��κ���y=$\frac{2}{3}$x2λ�ڵ�һ����ͼ���ϣ�����A0B1A1����A1B2A2��Ϊ�ȱ������Σ����A1B2A2�ı߳���������| A�� | $\frac{2}{3}$ | B�� | $\frac{4}{3}$ | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��A��ֱ�� | B�� | ��B��ֱ�� | C�� | ��C��ֱ�� | D�� | ���϶����� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com