

分析 (1)过C作CE⊥AB于E,根据等腰三角形的性质得到∠ACE=$\frac{1}{2}∠$ACB,AB=2AE,由已知条件得到∠ACE=∠ACD,根据角平分线的定义得到∠DAC=∠BAC,推出△ACD≌△ACE,根据全等三角形的性质得到AD=AE,于是得到结论;
(2)连接CE交BF于K,则K为△ABC的重心,设CK=2EK=2x,CE=BE=3x,根据角平分线的定义得到∠DAC=∠CAB=45°,推出△ACB是等腰直角三角形,由等腰直角三角形的性质得到CE⊥AB,AE=CE=BE,根据已知条件得到∠ACD=45°,推出△BEK≌△CEH,根据全等三角形的性质得到EK=CH=x,BK=EH=$\sqrt{10}$x,根据平行线分线段成比例定理得到$\frac{MH}{ME}=\frac{CH}{BE}=\frac{1}{3}$,求得MH=$\frac{1}{4}$EH=$\frac{\sqrt{10}}{4}$x,然后根据相似三角形的性质即可得到结论.
解答 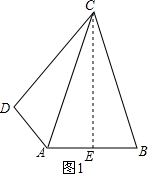 解:(1)过C作CE⊥AB于E,
解:(1)过C作CE⊥AB于E,
∵AC=BC,
∴∠ACE=$\frac{1}{2}∠$ACB,AB=2AE,
∵∠ACB=2∠ACD,
∴∠ACE=∠ACD,
∵AC平分∠BAD,
∴∠DAC=∠BAC,
在△ACD与△ACE中,
$\left\{\begin{array}{l}{∠DAC=∠EAC}\\{AC=AC}\\{∠DCA=∠ECA}\end{array}\right.$,
∴△ACD≌△ACE,
∴AD=AE,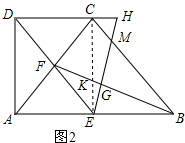
∴AB=2AD;
(2)连接CE交BF于K,则K为△ABC的重心,
∴设CK=2EK=2x,CE=BE=3x,
∵∠DAB=90°,AC平分∠DAB,
∴∠DAC=∠CAB=45°,
∵AC=BC,
∴△ACB是等腰直角三角形,
∴CE⊥AB,
∴AE=CE=BE,
∵∠ACB=2∠ACD,
∴∠ACD=45°,
∴AD=CD,∠ADC=90°,
∵EG⊥BF,
∴∠CEH=∠EBK,
在△BEK与△CEH中,
$\left\{\begin{array}{l}{∠ECH=∠KEB=90°}\\{BE=CE}\\{∠CEH=∠EBK}\end{array}\right.$,
∴△BEK≌△CEH,
∴EK=CH=x,BK=EH=$\sqrt{10}$x,
∵CH∥BE,∴$\frac{MH}{ME}=\frac{CH}{BE}=\frac{1}{3}$,
∴MH=$\frac{1}{4}$EH=$\frac{\sqrt{10}}{4}$x,
∵△BEG∽△BKH,
∴$\frac{BE}{BK}=\frac{EG}{KE}$,
∴EG=$\frac{2\sqrt{10}X}{10}$,
∴$\frac{MH}{EG}=\frac{5}{6}$.
点评 本题考查了相似三角形的判定和性质,等腰直角三角形的性质,全等三角形的判定和性质,等腰三角形的性质,证得△ABC是等腰直角三角形是解题的关键.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
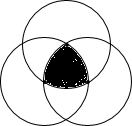 如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )
如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )| A. | 2π | B. | 2π-$\sqrt{3}$ | C. | 2π-2$\sqrt{3}$ | D. | 2π-3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
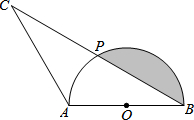 如图,已知AB是半圆O的直径,点P是半圆上一点,连结BP,并延长BP到点C,使PC=PB,连结AC.
如图,已知AB是半圆O的直径,点P是半圆上一点,连结BP,并延长BP到点C,使PC=PB,连结AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
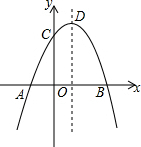 如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D.下列四个命题:①当x>0时,y>0; ②若a=-1,则b=3;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;④点C关于抛物线对称轴 的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6$\sqrt{2}$.其中正确的命题有( )个.
如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D.下列四个命题:①当x>0时,y>0; ②若a=-1,则b=3;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;④点C关于抛物线对称轴 的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6$\sqrt{2}$.其中正确的命题有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是一张长方形硬纸片,正好分成15个完全相同的小正方形,现要把它们剪切成3份,使每份有5个小正方形相连,折起来都可以围成一个没有盖的正方体纸盒.请在图中用实线画出一种剪切线.
如图是一张长方形硬纸片,正好分成15个完全相同的小正方形,现要把它们剪切成3份,使每份有5个小正方形相连,折起来都可以围成一个没有盖的正方体纸盒.请在图中用实线画出一种剪切线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | ±1 | D. | -$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com