
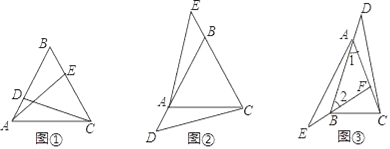
【题目】【感知】如图①,△ABC是等边三角形,点D、E分别在AB、BC边上,且AD=BE,易知:△ADC≌△BEA.
【探究】如图②,△ABC是等边三角形,点D、E分别在边BA、CB的延长线上,且AD=BE,△ADC与△BEA还全等吗?如果全等,请证明:如果不全等,请说明理由.
【拓展】如图③,在△ABC中,AB=AC,∠1=∠2,点D、E分别在BA、FB的延长线上,且AD=BE,若AF=![]() CF=2BE,S△ABF=6,则S△BCD的大小为 .
CF=2BE,S△ABF=6,则S△BCD的大小为 .
【答案】探究:△ADC与△BEA全等,理由见解析;拓展:S△BCD=13
【解析】试题分析:探究:利用平角的定义得出∠DAC=∠EBA即可得出结论;
拓展:先判断出△ADC≌△BEA,进而得出S△ADC=S△BEA,再利用同高的两三角形的面积的比等于底的比求出△ABE,△BCF的面积,即可得出结论.
试题解析:探究:△ADC与△BEA全等,
理由:在等边三角形ABC中,AB=AC,∠BAC=∠ABC=60°,
∴∠DAC=180°﹣∠BAC=120°,∠EBA=180°﹣∠ABC=120°,
∴∠DAC=∠EBA,
∵AD=BE,
∴△ADC≌△BEA;
拓展:∵∠1=∠2,
∴AF=BF,∠DAC=∠EBA,
∵AD=BE,AC=AB,
∴△ADC≌△BEA(SAS),
∴S△ADC=S△BEA,
∵AF=2BE,AF=BF,
∴BF=2BE,
∴S△ABE=![]() S△ABF=3(同高的两三角形的面积比是底的比),
S△ABF=3(同高的两三角形的面积比是底的比),
∴S△ADC=3,
∵AF=![]() CF,
CF,
∴S△BFC=![]() S△ABF=4(同高的两三角形的面积比是底的比),
S△ABF=4(同高的两三角形的面积比是底的比),
∴S△BCD=S△BCF+S△ABF+S△ADC=13,
故答案为13.


科目:初中数学 来源: 题型:
【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ) 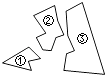
A.带①去
B.带②去
C.带③去
D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB是锐角,点D在射线BC上运动,连接AD,将线段AD绕点A逆时针旋转90°,得到AE,连接EC.
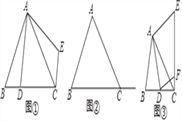
(1)操作发现:若AB=AC,∠BAC=90°,当D在线段BC上时(不与点B重合),如图①所示,请你直接写出线段CE和BD的位置关系和数量关系是_____,_____;
(2)猜想论证:
在(1)的条件下,当D在线段BC的延长线上时,如图②所示,请你判断(1)中结论是否成立,并证明你的判断.
(3)拓展延伸:
如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于_____度时,线段CE和BD之间的位置关系仍成立(点C、E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=3![]() 时,请直接写出线段CF的长的最大值是_____
时,请直接写出线段CF的长的最大值是_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com