
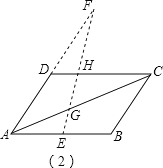
【题目】![]() ABCD中,点E是AB的中点,在直线AD上截取AF=2FD,EF交AC于G,则
ABCD中,点E是AB的中点,在直线AD上截取AF=2FD,EF交AC于G,则![]() =___________.
=___________.
【答案】![]() 或
或![]()
【解析】①点F在线段AD上时,设EF与CD的延长线交于H,
∵AB∥CD,
∴△EAF∽△HDF,
∴HD:AE=DF:AF=1:2,
即HD=![]() AE,
AE,
∵AB∥CD,
∴△CHG∽△AEG,
∴AG:CG=AE:CH
∵AB=CD=2AE,
∴CH=CD+DH=2AE+![]() AE=
AE=![]() AE,
AE,
∴AG:CG=2:5,
∴AG:(AG+CG)=2:(2+5),
即AG:AC=2:7;

②点F在线段AD的延长线上时,设EF与CD交于H,
∵AB∥CD,
∴△EAF∽△HDF,
∴HD:AE=DF:AF=1:2,
即HD=![]() AE,
AE,
∵AB∥CD,
∴△CHG∽△AEG,
∴AG:CG=AE:CH
∵AB=CD=2AE,
∴CH=CD-DH=2AE-![]() AE=
AE=![]() AE,
AE,
∴AG:CG=2:3,
∴AG:(AG+CG)=2:(2+3),
即AG:AC=2:5,
故答案为: ![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的长为6,宽为4,将长方形先向上平移2个单位,再向右平移2个单位得到长方形![]() ,则阴影部分面积是( )
,则阴影部分面积是( )
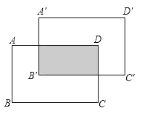
A.12B.10C.8D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,甲在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是( )米

A. 150 B. 175 C. 180 D. 225
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点(A点在B点左侧),与
轴交于A、B两点(A点在B点左侧),与![]() 轴交于点C,连接BC、AC,tan∠OCB -tan∠OCA=1,OB=4OA.
轴交于点C,连接BC、AC,tan∠OCB -tan∠OCA=1,OB=4OA.
(1)求![]() 和b的值;
和b的值;
(2)点E在线段BC上,点F在BC的延长线上,且BE=CF,点D是直线BC下方抛物线上一点,当△EDF是以EF为斜线的直角三角形,且4ED=3FD时,求D点坐标;
(3)在(2)的条件下,过点A作AG⊥![]() 轴,R为抛物线上CD段上一点,连接AR,点K在AR上,连接DK并延长交AG于点G,连接DR,且2∠RDK+∠RKD=90°,∠GAR=∠RDK,若点M(
轴,R为抛物线上CD段上一点,连接AR,点K在AR上,连接DK并延长交AG于点G,连接DR,且2∠RDK+∠RKD=90°,∠GAR=∠RDK,若点M(![]() )w为坐标平面内一点,直线MD与直线BC交于点N,当MN=DN时,求△MRD的面积.
)w为坐标平面内一点,直线MD与直线BC交于点N,当MN=DN时,求△MRD的面积.



查看答案和解析>>
科目:初中数学 来源: 题型:
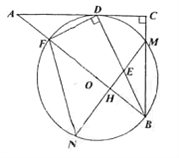
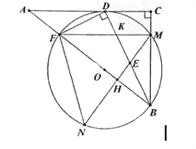
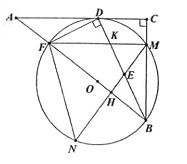
【题目】如图,在Rt△ABC中,∠C=90°,D为AC上一点,连接BD,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相较于点M,与AC相切于点D。过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连接FN.
(1)求证:BD平分∠ABC;
(2)连接FM与BD相交于点K,求证:MK=ME;
(3)若AF=1,tan∠N=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
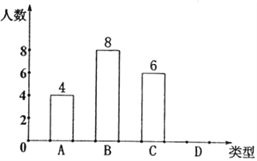
【题目】某校260名学生参加献爱心捐款活动,每人捐款4~7元,活动结束后随机抽查了20名学生每人的捐款数量,并按每人的捐款数量分为四种类型,A:捐款4元;B:捐款5元;C:捐款6元;D:捐款7元,并将其绘成如图所示的条形统计图.
(1)通过计算补全条形统计图;
(2)直接写出这20名学生每人捐款数量的众数和中位数;
(3)求这20名学生每人捐款数量的的平均数,并估计260名学生共捐款多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校为了创建“书香校园”,购买了一批图书,其中科普类图书平均每本的 价格比文学类图书平均每本的价格多4元,已知学校用16000元购买的科普类图书的本数与用12000元购买的文学类图书的本数相等.求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com