
【题目】如图,在△ABC中,BE平分∠ABC,DE∥BC.
(1)判断△DBE是什么三角形,并说明理由;
(2)若F为BE中点,∠ABE=30°,求∠BDF的度数.
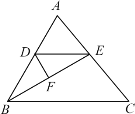
【答案】(1)△DBE是等腰三角形,理由见解析;(2)60°
【解析】
(1)如解图所示,根据角平分线的定义可得∠1=∠2,然后根据平行线的性质可得∠2=∠3,从而得出∠1=∠3,根据等角对等边即可得出结论;
(2)根据三线合一可得DF⊥BE,从而得出∠DFB=90°,然后根据三角形的内角和定理即可求出∠BDF的度数.
解:(1)△DBE是等腰三角形,理由如下.
∵ BE平分∠ABC,
∴ ∠1=∠2.
∵ DE∥BC,
∴ ∠2=∠3.
∴ ∠1=∠3.
∴ DB=DE.
即△DBE是等腰三角形.
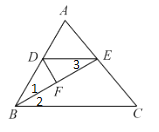
(2)∵ DB=DE,BF=EF.
∴ DF⊥BE,
即∠DFB=90°.
∵∠ABE=30°
∴∠BDF =180°-(∠ABE+∠DFB)=180°-(30°+90°)=60°.


科目:初中数学 来源: 题型:
【题目】某地在城区美化工程招标时,有甲、乙两个工程队投标.经测算,获得以下信息:
信息1:乙队单独完成这项工程需要60天;
信息2:若先由甲、乙两队合做16天,剩下的工程再由乙队单独做20天可以完成;
信息3:甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.
根据以上信息,解答下列问题:
(1)甲队单独完成这项工程需要多少天?
(2)若该工程计划在50天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲、乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在所给坐标系中画出二次函数y=x2+bx+c的图象.
(4)写出当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承包了某标段全长1800米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进2米,经过5天施工,两组共掘进了60米.
(1)求甲、乙两班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进2米,乙组平均每天能比原来多掘进1米.按此施工进度,能够比原来少用多少天完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() 连接AC,BD交于点M,AC与OD相交于E,BD与OA相较于F,连接OM,则下列结论中:①
连接AC,BD交于点M,AC与OD相交于E,BD与OA相较于F,连接OM,则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④MO平分
;④MO平分![]() ,正确的个数有( )
,正确的个数有( )
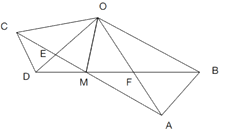
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
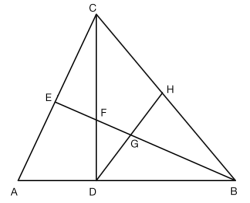
【题目】如图,![]() 是
是![]() 的两条高线,且它们相交于
的两条高线,且它们相交于![]() 是
是![]() 边的中点,连结
边的中点,连结![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,已知
,已知![]() .
.
(1)求证BF=AC.
(2)若BE平分![]() .
.
①求证:DF=DG.
②若AC=8,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
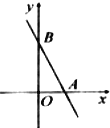
【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 点,
点,![]() ,且
,且![]() 满足
满足![]() ,点
,点![]() 在直线
在直线![]() 的左侧,且
的左侧,且![]() .
.
(1)求![]() 的值;
的值;
(2)若点![]() 在
在![]() 轴上,求点
轴上,求点![]() 的坐标;
的坐标;
(3)若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
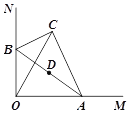
【题目】如图,在Rt△ABC中,BC![]() 2,∠BAC
2,∠BAC![]() 30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动,下列结论: ①若C,O两点关于AB对称,则OA
30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动,下列结论: ①若C,O两点关于AB对称,则OA![]() ;②C,O两点距离的最大值为4;③若AB平分CO,则AB⊥CO;④斜边AB的中点D运动路径的长为
;②C,O两点距离的最大值为4;③若AB平分CO,则AB⊥CO;④斜边AB的中点D运动路径的长为![]() .
.
其中正确的是( )
A. ①② B. ①②③ C. ①③④ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com