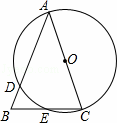
如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点D，交BC于点E．
（1）求证：BE=CE；
（2）若BD=2，BE=3，求AC的长．
科目：初中数学 来源： 题型：
甲、乙两布袋装有红、白两种小球，两袋装球总数量相同，两种小球仅颜色不同．甲袋中，红球个数是白球个数的2倍；乙袋中，红球个数是白球个数的3倍，将乙袋中的球全部倒入甲袋，随机从甲袋中摸出一个球，摸出红球的概率是（ ）
|
| A． |
| B． |
| C． |
| D． |
|
查看答案和解析>>
科目：初中数学 来源： 题型：
阅读理解
抛物线y=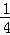
x2上任意一点到点（0，1）的距离与到直线y=﹣1的距离相等，你可以利用这一性质解决问题．
问题解决
如图，在平面直角坐标系中，直线y=kx+1与y轴交于C点，与函数y=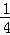x2的图象交于A，B两点，分别过A，B两点作直线y=﹣1的垂线，交于E，F两点．
（1）写出点C的坐标，并说明∠ECF=90°；
（2）在△PEF中，M为EF中点，P为动点．
①求证：PE2+PF2=2（PM2+EM2）；
②已知PE=PF=3，以EF为一条对角线作平行四边形CEDF，若1＜PD＜2，试求CP的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
已知椭圆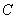
：
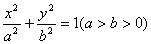，左、右两个焦点分别为
、
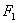，上顶点
，
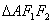为正三角形且周长为6.
（1）求椭圆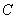的标准方程及离心率；
（2）
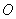为坐标原点，
是直线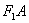
上的一个动点，求
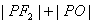的最小值，并求出此时点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
=
，即
=
，
的绝对值等于（ ）
+
．
