
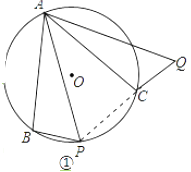
【题目】已知⊙O中,弦AB=AC,点P是∠BAC所对弧上一动点,连接PA,PB.
(1)如图①,把△ABP绕点A逆时针旋转到△ACQ,连接PC,求证:∠ACP+∠ACQ=180°;
(2)如图②,若∠BAC=60°,试探究PA、PB、PC之间的关系.
(3)若∠BAC=120°时,(2)中的结论是否成立?若是,请证明;若不是,请直接写出它们之间的数量关系,不需证明.
【答案】
(1)
证明:如图①,连接PC.
∵△ACQ是由△ABP绕点A逆时针旋转得到的,
∴∠ABP=∠ACQ.
由图①知,点A、B、P、C四点共圆,
∴∠ACP+∠ABP=180°(圆内接四边形的对角互补),
∴∠ACP+∠ACQ=180°(等量代换);
(2)
证明:解:PA=PB+PC.理由如下:
如图②,连接BC,延长BP至E,使PE=PC,连接CE.
∵弦AB=弦AC,∠BAC=60°,
∴△ABC是等边三角形(有一内角为60°的等腰三角形是等边三角形).
∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°(圆内接四边形的对角互补),
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,
∵PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=∠ECP=∠EPC=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP(等量代换).
在△BEC和△APC中,  ,
,
∴△BEC≌△APC(SAS),
∴BE=PA,
∴PA=BE=PB+PC;

(3)
证明:若∠BAC=120°时,(2)中的结论不成立. ![]() PA=PB+PC.理由如下:
PA=PB+PC.理由如下:
如图③,在线段PC上截取PQ,使PQ=PB,过点A作AG⊥PC于点G.
∵∠BAC=120°,∠BAC+∠BPC=180°,
∴∠BPC=60°.
∵弦AB=弦AC,
∴∠APB=∠APQ=30°.
在△ABP和△AQP中,
∵  ,
,
∴△ABP≌△AQP(SAS),
∴AB=AQ,PB=PQ(全等三角形的对应边相等),
∴AQ=AC(等量代换).
在等腰△AQC中,QG=CG.
在Rt△APG中,∠APG=30°,则AP=2AG,PG= ![]() AG.
AG.
∴PB+PC=PG﹣QG+PG+CG=PG﹣QG+PG+QG=2PG=2 ![]() AG,
AG,
∴ ![]() PA=2
PA=2 ![]() AG,即
AG,即 ![]() PA=PB+PC.
PA=PB+PC.

【解析】(1)如图①,连接PC.根据“内接四边形的对角互补的性质”即可证得结论;(2)如图②,通过作辅助线BC、PE、CE(连接BC,延长BP至E,使PE=PC,连接CE)构建等边△PCE和全等三角形△BEC≌△APC;然后利用全等三角形的对应边相等和线段间的和差关系可以求得PA=PB+PC;(3)如图③,在线段PC上截取PQ,使PQ=PB,过点A作AG⊥PC于点G.利用全等三角形△ABP≌△AQP(SAS)的对应边相等推知AB=AQ,PB=PG,将PA、PB、PC的数量关系转化到△APC中来求即可.


科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点P是BC的中点,仅用无刻度的直尺按要求画图:
(1)在图①中画出AD的中点M; 
(2)在图②中画出对角线AC的三等分点E,点F. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒. 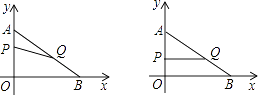
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
(3)当t为何值时,△APQ的面积为 ![]() 个平方单位?
个平方单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,AD是∠BAC的平分线.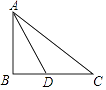
(1)尺规作图:过点D作DE⊥AC于E;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(方案设计题)如图是人民公园中的荷花池,现要测量荷花池岸边树A与树B间的距离.如果直接测量比较困难,请你根据所学知识,以卷尺和测角仪为测量工具,设计两种不同的测量方案并画出图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△EFG≌△NMH, ∠F与∠M是对应角.

(1)写出相等的线段与相等的角;
(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB∥DC,连接BD,BE平分∠ABD,BE⊥AD,∠EBC和∠DCB的角平分线相交于点F,若∠ADC=110°,则∠F的度数为( )
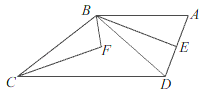
A. 115° B. 110° C. 105° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)当该方程的一个根为1时,求a的值及方程的另一根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com