
【题目】(方案设计题)如图是人民公园中的荷花池,现要测量荷花池岸边树A与树B间的距离.如果直接测量比较困难,请你根据所学知识,以卷尺和测角仪为测量工具,设计两种不同的测量方案并画出图形.

 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】如果,矩形ABCD中,点E在AB上,点F在CD上,点G,H在对角线AC上,且CH=AG,CF=AE. 
(1)求证:△AGE≌△CHF;
(2)若AB=8,AD=4,且GH恰好平分∠FGE,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
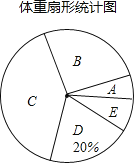
【题目】某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:
体重频数分布表
组边 | 体重(千克) | 人数 |
A | 45≤x<50 | 12 |
B | 50≤x<55 | m |
C | 55≤x<60 | 80 |
D | 60≤x<65 | 40 |
E | 65≤x<70 | 16 |
(1)填空:①m=__(直接写出结果);
②在扇形统计图中,C组所在扇形的圆心角的度数等于__度;
(2)如果该校九年级有1000名学生,请估算九年级体重低于60千克的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O中,弦AB=AC,点P是∠BAC所对弧上一动点,连接PA,PB.
(1)如图①,把△ABP绕点A逆时针旋转到△ACQ,连接PC,求证:∠ACP+∠ACQ=180°;
(2)如图②,若∠BAC=60°,试探究PA、PB、PC之间的关系.
(3)若∠BAC=120°时,(2)中的结论是否成立?若是,请证明;若不是,请直接写出它们之间的数量关系,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD⊥AB于点D,BE⊥AC于点E,CD、BE交于点O,且AO平分∠BAC,则图中的全等三角形共有( )
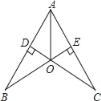
A. 1对 B. 2对 C. 3对 D. 4对
查看答案和解析>>
科目:初中数学 来源: 题型:
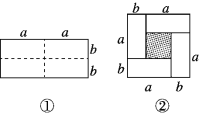
【题目】动手操作:如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.
提出问题:
(1)观察图②,请用两种不同的方法表示阴影部分的面积:_____________,_____________;
(2)请写出三个代数式(a+b)2,(a-b)2,ab之间的一个等量关系:___________________________;
问题解决:根据上述(2)中得到的等量关系,解决下列问题:已知x+y=8,xy=7,求x-y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是高,AF是△ABC外角∠CAD的平分线. 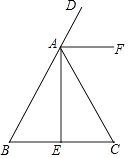
(1)用尺规作图:作∠AEC的平分线EN(保留作图痕迹,不写作法和证明);
(2)设EN与AF交于点M,判断△AEM的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以x为自变量的二次函数y=﹣x2+(2m+2)x﹣(m2+4m﹣3)中,m为不小于0的整数,它的图象与x轴的交点A在原点左边,交点B在原点右边.
(1)求这个二次函数的解析式;
(2)设点C为此二次函数图象上的一点,且满足△ABC的面积等于10,请求出点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com