
【题目】求下列各式中的x:
(1)16x2-361=0; (2)(x-1)2=25;
(3)27![]() =216; (4)
=216; (4)![]() (x-2)3=
(x-2)3=![]() .
.
【答案】(1)x=±![]() ;(2)x=-4或6;(3)x=
;(2)x=-4或6;(3)x=![]() ;(4)x=2+
;(4)x=2+![]() .
.
【解析】
(1)移项开方,然后通过解关于x的一元一次方程可以求得x的值;(2)直接开方,然后通过解关于x的一元一次方程可以求得x的值;(3) 方程两边同除以27,然后直接开立方求解即可;(4)首先化简,而后直接开立方求解.
(1)移项,得16x2=361,
方程两边同除以16,得x2=![]() ,
,
开平方,得x=±![]() .
.
(2)开平方,得x-1=±5,
由x-1=5解得x=6,
由x-1=-5解得x=-4,
即x=-4或6.
(3)方程两边同除以27,得![]() =8;
=8;
开立方,得8x-![]() =2,
=2,
解得x=![]() .
.
(4)化简方程,得(x-2)3=15,开立方,
得x-2=![]() ,解得x=2+
,解得x=2+![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】综合题。
(1)解方程:x2=2x.
(2)如图,Rt△ABC中,∠BAC=90°,AB=5,AC=12,将△ABC向右平移至△A′B′C′的位置,使得四边形ABB′A′为菱形,求B′C的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )

A.2010年至2014年间工业生产总值逐年增加
B.2014年的工业生产总值比前一年增加了40亿元
C.2012年与2013年每一年与前一年比,其增长额相同
D.从2011年至2014年,每一年与前一年比,2014年的增长率最大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒. 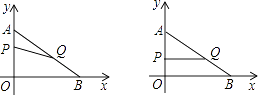
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
(3)当t为何值时,△APQ的面积为 ![]() 个平方单位?
个平方单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于下列各组条件,不能判定△![]() ≌△
≌△![]() 的一组是 ( )
的一组是 ( )
A. ∠A=∠A′,∠B=∠B′,AB=A′B′
B. ∠A=∠A′,AB=A′B′,AC=A′C′
C. ∠A=∠A′,AB=A′B′,BC=B′C′
D. AB=A′B′,AC=A′C′,BC=B′C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(方案设计题)如图是人民公园中的荷花池,现要测量荷花池岸边树A与树B间的距离.如果直接测量比较困难,请你根据所学知识,以卷尺和测角仪为测量工具,设计两种不同的测量方案并画出图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问 ![]() 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x﹣3与y轴交于点A,点A与点B关于x轴对称,过点B作y轴的垂线l,直线l与直线y=2x﹣3交于点C.
(1)求点C的坐标;
(2)如果抛物线y=nx2﹣4nx+5n(n>0)与线段BC有唯一公共点,求n的取值范围. 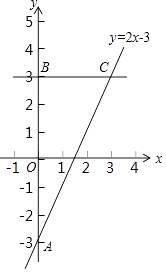
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com