
【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问 ![]() 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
【答案】
(1)
解:①∵A(﹣2,0),C(0,﹣4)在抛物线上,
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=x2﹣4;
②如图1,连接DB、OP,设P(x,x2﹣4),
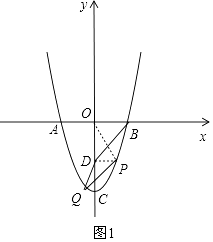
∵A(﹣2,0),对称轴为y轴,
∴B(2,0),
∴S△BDP=S△ODP+S△OBP﹣S△BOD= ![]() OD|x|+
OD|x|+ ![]() OB|x2﹣4|﹣
OB|x2﹣4|﹣ ![]() ODOB=x+4﹣x2﹣2=﹣x2+x+2=﹣(x﹣
ODOB=x+4﹣x2﹣2=﹣x2+x+2=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∵点P在第四象限运动,
∴0<x<2,
∴当x= ![]() 时,S△BDP有最大值
时,S△BDP有最大值 ![]() ,当x=2时,S△BDP有最小值0,
,当x=2时,S△BDP有最小值0,
∴0<S△BDP≤ ![]() ,
,
∵四边形BDQC为平行四边形,
∴S四边形BDQP=2S△BDP,
∴0<S四边形BDQP≤ ![]() ;
;
(2)
解:如图2,过点P作PG⊥AB,设A(x1,0),B(x2,0),P(x,y),
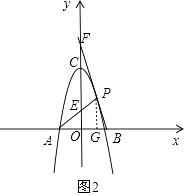
∵PG∥y轴,
∴△AOE∽△AGP,△BGP∽△BOF,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() =
= ![]() ,
,
当y=0时,可得ax2+c=0,
∴x1+x2=0,x1x2= ![]() ,
,
∴ ![]() +
+ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴OE+OF=2c,
∴ ![]() =
= ![]() =2,
=2,
∴ ![]() =
= 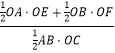 =
= 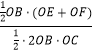 =
= ![]() =1,
=1,
∴ ![]() 的值与a,c无关,比值为1.
的值与a,c无关,比值为1.
【解析】(1)①由A、C两点的坐标,利用待定系数法可求得抛物线解析式;②连接BD、OP,设出P点坐标,利用S△BDP=S△ODP+S△OBP﹣S△BOD可用x表示出四边形BDQP的面积,借助x的取值范围,可求得四边形BDQP面积的取值范围;(2)过点P作PG⊥AB,设A(x1 , 0),B(x2 , 0),P(x,y),由△AOE∽△AGP、△BGP∽△BOF,利用相似三角形的性质和一元二次方程根与系数的关系可整理得到 ![]() =2,再利用三角形的面积可得
=2,再利用三角形的面积可得 ![]() 的值.
的值.
【考点精析】认真审题,首先需要了解相似三角形的性质(对应角相等,对应边成比例的两个三角形叫做相似三角形).


科目:初中数学 来源: 题型:
【题目】如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF. 
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD⊥AB于点D,BE⊥AC于点E,CD、BE交于点O,且AO平分∠BAC,则图中的全等三角形共有( )
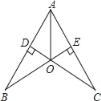
A. 1对 B. 2对 C. 3对 D. 4对
查看答案和解析>>
科目:初中数学 来源: 题型:
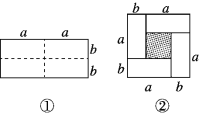
【题目】动手操作:如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.
提出问题:
(1)观察图②,请用两种不同的方法表示阴影部分的面积:_____________,_____________;
(2)请写出三个代数式(a+b)2,(a-b)2,ab之间的一个等量关系:___________________________;
问题解决:根据上述(2)中得到的等量关系,解决下列问题:已知x+y=8,xy=7,求x-y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是高,AF是△ABC外角∠CAD的平分线. 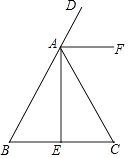
(1)用尺规作图:作∠AEC的平分线EN(保留作图痕迹,不写作法和证明);
(2)设EN与AF交于点M,判断△AEM的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( ) 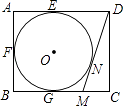
A.![]()
B.![]()
C.![]()
![]()
D.2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com