
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( ) 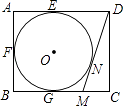
A.![]()
B.![]()
C.![]()
![]()
D.2 ![]()
【答案】A
【解析】解:连接OE,OF,ON,OG,
在矩形ABCD中,
∵∠A=∠B=90°,CD=AB=4,
∵AD,AB,BC分别与⊙O相切于E,F,G三点,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°,
∴四边形AFOE,FBGO是正方形,
∴AF=BF=AE=BG=2,
∴DE=3,
∵DM是⊙O的切线,
∴DN=DE=3,MN=MG,
∴CM=5﹣2﹣MN=3﹣MN,
在Rt△DMC中,DM2=CD2+CM2 ,
∴(3+NM)2=(3﹣NM)2+42 ,
∴NM= ![]() ,
,
∴DM=3 ![]() =
= ![]() ,
,
故选A.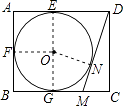
【考点精析】利用矩形的性质和切线的性质定理对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问 ![]() 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x﹣3与y轴交于点A,点A与点B关于x轴对称,过点B作y轴的垂线l,直线l与直线y=2x﹣3交于点C.
(1)求点C的坐标;
(2)如果抛物线y=nx2﹣4nx+5n(n>0)与线段BC有唯一公共点,求n的取值范围. 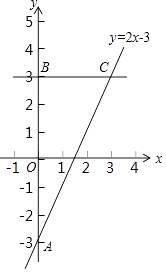
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于概率,下列说法正确的是( )
A.莒县“明天降雨的概率是75%”表明明天莒县会有75%的时间会下雨
B.随机抛掷一枚质地均匀的硬币,落地后一定反面向上
C.在一次抽奖活动中,中奖的概率是1%,则抽奖100次就一定会中奖
D.同时抛掷两枚质地均匀硬币,“一枚硬币正面向上,一枚硬币反面向上”的概率是 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某闭合电路中,其两端电压恒定,电流I(A)与电阻R(Ω)图象如图所示,回答问题: 
(1)写出电流I与电阻R之间的函数解析式.
(2)如果一个用电器的电阻为5Ω,其允许通过的最大电流是1A,那么这个用电器接在这个闭合电路中,会不会烧毁?说明理由.
(3)若允许的电流不超过4A时,那么电阻R的取值应该控制在什么范围?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com