
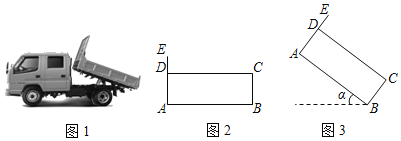
【题目】如图1,是一种自卸货车.如图2是货箱的示意图,货箱是一个底边AB水平的矩形,AB=8米,BC=2米,前端档板高DE=0.5米,底边AB离地面的距离为1.3米.卸货时,货箱底边AB的仰角α=37°(如图3),求此时档板最高点E离地面的高度.(精确到0.1米,参考值:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
【答案】点E离地面的高度为8.1米
【解析】
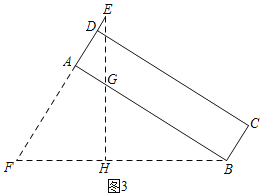
延长DA交水平虚线于F,过E作EH⊥BF于H,根据题意,在Rt△ABF中,求出AF,从而得到EF,结合Rt△EFH,求出EH即可求得结果.
解:如图3所示,延长DA交水平虚线于F,过E作EH⊥BF于H,
∵∠BAF=90°,∠ABF=37°,
∴Rt△ABF中,AF=tan37°×AB≈0.75×8=6(米),
∴EF=AF+AD+DE=8.5,
∵∠EHF=90°=∠BAF,∠BFA=∠EFH,
∴∠E=37°,
∴Rt△EFH中,EH=cos37°×EF≈0.80×8.5=6.8(米),
又∵底边AB离地面的距离为1.3米,
∴点E离地面的高度为6.8+1.3=8.1(米),
故答案为:8.1米.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】2017年全球超级计算机500强名单公布,中国超级计算机“神威·太湖之光”和“天河二号”携手夺得前两名.已知“神威·太湖之光”的浮点运算速度是“天河二号”的2.74倍.这两种超级计算机分别进行100亿亿次浮点运算,“神威·太湖之光”的运算时间比“天河二号”少18.75秒,求这两种超级计算机的浮点运算速度.设“天河二号”的浮点运算速度为![]() 亿亿次/秒,依题意,可列方程为___________.
亿亿次/秒,依题意,可列方程为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
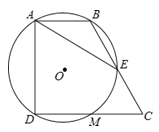
【题目】如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:
①DM=CM;②弧AB=弧EM;③⊙O的直径为2;④AE=AD.
其中正确的结论有______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,则球的半径长是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在
在![]() 的边
的边![]() 上,以
上,以![]() 为圆心,
为圆心,![]() 为半径的圆与
为半径的圆与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,并且与边
,并且与边![]() 相切于点
相切于点![]() ,连接
,连接![]() .已知
.已知![]() 平分
平分![]() .
.
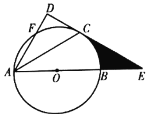
(1)求证:![]() ;
;
(2)若![]() ,
,![]() 的半径为3.求阴影部分的面积.(结果保留
的半径为3.求阴影部分的面积.(结果保留![]() 和根号)
和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学共有学生2000名,各年级男、女生人数如下表:
年级 | 六年级 | 七年级 | 八年级 | 九年级 |
男生 | 250 | z | 254 | 258 |
女生 | x | 244 | y | 252 |
若从全校学生中任意抽取一名,抽到六年级女生的概率是0.12;若将各年级的男、女学生人数制成扇形统计图,八年级女生对应扇形的圆心角为44.28°.
(1)求x,y,z的值;
(2)求各年级女生的平均数;
(3)如果从八年级随机抽取36名学生参加社会实践活动,求抽到八年级某同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
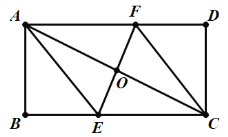
【题目】如图,矩形ABCD中,AB=4,BC=8,过对角线AC中点O的直线分别交BC、AD边于点E、F.
(1)求证:四边形AECF是平行四边形;
(2)当四边形AECF是菱形时,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y![]() (k>0,x>0)的图象经过AC的中点D,则k的值为( )
(k>0,x>0)的图象经过AC的中点D,则k的值为( )

A.4B.5C.6D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com