
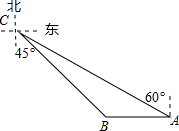
 如图,码头A在码头B的正东方向,两个码头之间的距离为32海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,求码头A与小岛C的距离.($\sqrt{3}$≈1.732,结果精确到0.01海里)
如图,码头A在码头B的正东方向,两个码头之间的距离为32海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,求码头A与小岛C的距离.($\sqrt{3}$≈1.732,结果精确到0.01海里) 分析 根据正切函数,可得CD的长,根据直角三角形的性质,可得答案.
解答 解:作CD⊥AB交AB延长线于点D,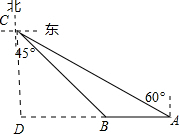
∠D=90°
由题意,得∠DCB=45°,∠CAD=90°-60°=30°,AB=32海里,
设CD=x海里,在Rt△DCB中,tan∠DCB=$\frac{BD}{CD}$,tan45°=$\frac{BD}{x}$=1,
BD=x,AD=AB+BD=32+x,tan30°=$\frac{x}{x+32}$=$\frac{\sqrt{3}}{3}$,
解得x=16$\sqrt{3}$+16,
∵∠CAD=30°,∠CDA=90°,
∴AC=2CD=32$\sqrt{3}$+32≈87.42海里,
答:码头A与小岛C的距离约为87.42海里.
点评 本题考查了解直角三角形,利用了锐角三角函数,直角三角形的性质,画出直角三角形得出CD的长是解题关键.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{450}{x}$=$\frac{330}{x+35}$×2 | B. | $\frac{450}{x}$=$\frac{330}{2x}$-35 | C. | $\frac{450}{x}$-$\frac{330}{2x}$=35 | D. | $\frac{330}{x}$-$\frac{450}{2x}$=35 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x人 | 500 | 1000 | 1500 | 2000 | 2500 | 3000 |
| y元 | -3000 | -2000 | -1000 | 0 | 1000 | 2000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com