
���ⱳ����

��ͼ��1�������ı���ABCD�У�AB=AD����BAD=120�㣬��B=��ADC=90�㣮E��F�ֱ���BC��CD�ϵĵ㣮�ҡ�EAF=60�㣬̽��EF��BE��FD��������ϵ�����Һ��ŷ���λͬѧ̽����˼·��Ȼ������ͬ�������ó�����ȷ�Ľ��ۣ�
������������ģ��ѡ�ABE���ŵ�A��ʱ����ת��ʹAB��AD�غϣ��á�ADG����ȷ����F��D��G��һ��ֱ���ϣ���֤����AEF��AGF��
�ŷ���������ģ��ӳ�FD����G��ʹDG=BE������AG����֤����ABE�ա�ADG����AEF�ա�AGF�����ǵó��Ľ�����_________________��
��2��̽�����죺
��ͼ��2���������ı���ABCD�У�AB=AD����B+��D=180�㣮E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF= ��BAD����1���еĽ����Ƿ���Ȼ��������˵�����ɣ�
��BAD����1���еĽ����Ƿ���Ȼ��������˵�����ɣ�
��3��ʵ��Ӧ�ã�
��ͼ��3������ij�ξ�����ϰ�У���ͧ����ָ�����ģ�O������ƫ��30���A������ͧ����ָ�����ģ�O������ƫ��70���B������������ͧ��ָ�����ĵľ��붼��90����ӵ��ж�ָ���ͧ��������������60����/Сʱ���ٶ�ǰ����ͬʱ����ͧ����������BM�ķ���OBF=120�㣩����14����/Сʱ���ٶ�ǰ��1.5Сʱ��ָ�����Ĺ۲�ס�������ͧ�ֱ�E��F�����ҽ�ͧ����ָ��������ƫ��80�㣬���ʣ�����ͧE��F֮��ľ����Ƿ���ϣ�2����������������ϣ����������֮ͧ��ľ��루���������ߣ�����������ϣ���˵�����ɣ�
 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016�캣�϶������п�ģ�⣨һ����ѧ�Ծ��������棩 ���ͣ������
����ز��Ż�Ϥ��2010�꺣��ʡ�߿�����������54741�ˣ���ͼ�DZ�����������ͳ��ͼ��

����������Ϣ������������⣺
��1��2010�꺣��ʡ�߿����������У�������� �ˣ�
��2���벹������ͼ�е�����ͳ��ͼ������ͳ��ͼ���ٷ��ʾ�ȷ��0.1%����
��3�����������ͼ������ͳ��ͼ������Ϊ��ʷ�����Ӧ������Բ�Ľ�ӦΪ �㣨��ȷ��1�㣩��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�캣�������λ���ѧ�п�ģ�⣨һ����ѧ�Ծ��������棩 ���ͣ�ѡ����
�ƶ��������Ѿ�ȫ��������ǵ��ճ������ֹ2015��3�£�ȫ��4G�û������ﵽ1.62�ڣ�����1.62���ÿ�ѧ��������ʾΪ�� ��
A��1.62��104B��1.62��106C��1.62��108D��0.162��109
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016��ӱ������ж������п�һģ��ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ���ı���OABC�Ǿ��Σ��ı���CDEF�������Σ���C��D��x����������ϣ���A��y����������ϣ���F��BC�ϣ���B��E�ڷ���������y= ��ͼ���ϣ�OA=2��OC=1����������CDEF�����Ϊ�� ��
��ͼ���ϣ�OA=2��OC=1����������CDEF�����Ϊ�� ��

A��4 B��1 C��3 D��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016��ӱ������ж������п�һģ��ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ���������ϱ�ʾ�� ������5���ĵ�����ǣ� ��
������5���ĵ�����ǣ� ��

A����E B����F C����P D����Q
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016��ӱ�������Ƥ���п�ģ����ѧ�Ծ��������棩 ���ͣ������
�Ȼ������ʽ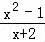 ��
�� �����ж��������ʽ3x+2�Ĵ�С��ϵ��
�����ж��������ʽ3x+2�Ĵ�С��ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016��ӱ�������Ƥ���п�ģ����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ���ھ���ABCD�У�AB= ��AD=1���Ѹþ����Ƶ�A˳ʱ����ת���ȵþ���AB��C��D�䣬��C������AB���ӳ����ϣ���ͼ����Ӱ���ֵ�����ǣ� ��
��AD=1���Ѹþ����Ƶ�A˳ʱ����ת���ȵþ���AB��C��D�䣬��C������AB���ӳ����ϣ���ͼ����Ӱ���ֵ�����ǣ� ��

A��
 B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�찲��ʡ�ߺ����п���ģ�Ծ���ѧ�Ծ��������棩 ���ͣ������
��ͼ��ʾ��CDΪ��O��ֱ������B�ڡ�O�ϣ�����BC��BD������B������AE��CD���ӳ��߽��ڵ�A��OE��BD����BC�ڵ�F����AB�ڵ�E��

��1����֤����E=��C��
��2������O�İ뾶Ϊ3��AD=2������OE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016�츣��������̩���п�ģ���Ծ���ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ����һ������ֱ�����ǰ尴����ͼ��ʽ��������һ������ֽƬ�ϣ����СϦ�=24�㣬��ϦµĶ���Ϊ�� ��

A��24�� B��21�� C��30�� D��45��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com