
���� ��1�������Ϊx�������۵���Ϊ3000-10��x-10��Ԫ���������۵���ǡ��Ϊ2500Ԫ���з�����⣻
��2��������y=�����۵���-�ɱ����ۣ��������������۵��۾�������2600Ԫ����0��x��10��10��x��60��x��60��������г�������ϵʽ��
��� �⣺��1�����̼�һ�ι�����ֲ�Ʒx��ʱ�����۵���ǡ��Ϊ2500Ԫ��
�������3000-10��x-10��=2500��
���x=60��
���̼�һ�ι�����ֲ�Ʒ60��ʱ�����۵���ǡ��Ϊ2500Ԫ��
��2����0��x��10ʱ��y=��3000-2300��x=700x��
��10��x��60ʱ��y=x[3000-10��x-10��-2300]=-10x2+800x��
��x��60ʱ��y=��2500-2300��x=200x��
����y=$\left\{\begin{array}{l}{700x��0��x��10����x������}\\{-10{x}^{2}+800x��10��x��60����x������}\\{200x��x��60����x������}\end{array}\right.$��
���� ���⿼���˶��κ��������ã��ؼ�����ȷ���۵��������ۼ���֮��ĺ�����ϵʽ������ﵥ��������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
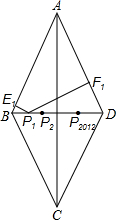 ��ͼ����֪����ABCD�ı�AB=10���Խ���BD=12��BD������2013����ͬ�ĵ�P1��P2��P3��P2013����Pi��i=1��2��3������PiEi��Ei��PiEi��Fi��P1E1+P1F1+P2E2+P2F2+��P2012E2012+P2012F2012+P2013E2013+P2013F2013��ֵΪ19324.8��
��ͼ����֪����ABCD�ı�AB=10���Խ���BD=12��BD������2013����ͬ�ĵ�P1��P2��P3��P2013����Pi��i=1��2��3������PiEi��Ei��PiEi��Fi��P1E1+P1F1+P2E2+P2F2+��P2012E2012+P2012F2012+P2013E2013+P2013F2013��ֵΪ19324.8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ������֤������proofs without words�������ǽ���ѧ�����ü��д��������������ļ���ͼ�������֣��ֽ��߳�Ϊa����������ȥһ���߳�Ϊb��С�����Σ�a��b������ͼ�ף�����ʣ�µIJ���ƴ��һ�����Σ���ͼ�ң�������������ͼ������Ӱ���ֵ�������ܹ���֤�ĵ�ʽ�ǣ�������
������֤������proofs without words�������ǽ���ѧ�����ü��д��������������ļ���ͼ�������֣��ֽ��߳�Ϊa����������ȥһ���߳�Ϊb��С�����Σ�a��b������ͼ�ף�����ʣ�µIJ���ƴ��һ�����Σ���ͼ�ң�������������ͼ������Ӱ���ֵ�������ܹ���֤�ĵ�ʽ�ǣ�������| A�� | a2-b2=��a+b����a-b�� | B�� | ��a-b��2=a2-2ab+b2 | ||
| C�� | ��a+2b����a-b��=a2+ab-2b2 | D�� | ��a+b��2=a2+2ab+b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
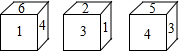 ��һ�����壬�������Ϸֱ�д������1��2��3��4��5��6���������˴Ӳ�ͬ�ĽǶȹ۲�Ľ����ͼ��ʾ�������1�Ķ��������Ϊa��3�Ķ��������Ϊb����ôa+b��ֵΪ��������
��һ�����壬�������Ϸֱ�д������1��2��3��4��5��6���������˴Ӳ�ͬ�ĽǶȹ۲�Ľ����ͼ��ʾ�������1�Ķ��������Ϊa��3�Ķ��������Ϊb����ôa+b��ֵΪ��������| A�� | 3 | B�� | 7 | C�� | 8 | D�� | 11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com