
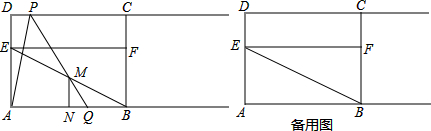
���� ��1������P��PH��ֱ��AB�����⺬30���ֱ�����������HB������DP���ɣ�
��2���ٷ����������0��t��3ʱ��Q�ڵ�B�������غ�ʱ���ڵ�3��t��5ʱ����H����F��������غ�ʱ���۵�t��9������K�ڵ�F���Ҳ࣬�ֱ���⼴�ɣ�
��3������������ٵ�MN=BN=3ʱ�ڵ�BM=BN=3ʱ�۵�MN=MBʱ�ֱ���⼴�ɣ�
��� �⣺��1����ͼ1������P��PH��ֱ��AB��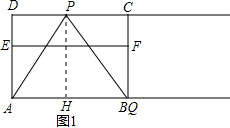
�ߡ�PQA=60�㣬AD=3$\sqrt{3}$��
��PH=3$\sqrt{3}$��
��HB=CP=$\frac{PH}{tan60��}$=3��
��DP=DC-CP=6-3=3��
��2�����APQ���ı���ABFE���ص����ֵ����ΪS��
����ͼ2��0��t��3��Q�ڵ�B�������غ�ʱ��MΪDC���е㣬����MB��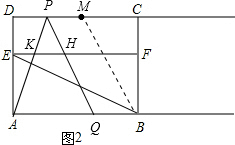
S=S��APQ-S��KHP=$\frac{1}{2}$AQ•AD-$\frac{1}{2}$KH•DE=$\frac{1}{2}$��[6-��3-t��]��3$\sqrt{3}$-$\frac{1}{2}$��$\frac{1}{3}$��[6-��3-t��]��$\sqrt{3}$=$\frac{4\sqrt{3}}{3}$t+4$\sqrt{3}$��
����ͼ3����3��t��5ʱ����H����F��������غ�ʱ��MΪDC���е㣬����MB��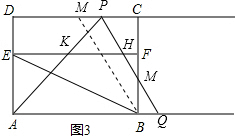
��APQ���ı���ABFE���ص����ֵ����
S=S��APQ-S��KHP-S��BQM=$\frac{1}{2}$AQ•AD-$\frac{1}{2}$KH•DE-$\frac{1}{2}$BQ•BM=$\frac{1}{2}$[6+��t-3��]��3$\sqrt{3}$-$\frac{1}{2}$[6+��t-3��]��$\sqrt{3}$-$\frac{1}{2}$��t-3����$\sqrt{3}$��t-3��=-$\frac{\sqrt{3}}{2}$t2+$\frac{13\sqrt{3}}{3}$t-$\frac{\sqrt{3}}{2}$��
����ͼ4����5��t��9����H����F����Ҳ࣬K����F������ʱ��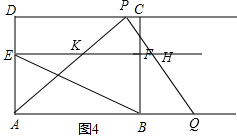
��APQ���ı���ABFE���ص����ֵ����S=S�ı���ABFE-S��AKE=AB•AE-$\frac{1}{2}$EK•AE=6��2$\sqrt{3}$-$\frac{1}{2}$��$\frac{2}{3}$t��2$\sqrt{3}$=-$\frac{2\sqrt{3}}{3}$t+12$\sqrt{3}$��
����ͼ5����t��9������K�ڵ�F���Ҳ࣬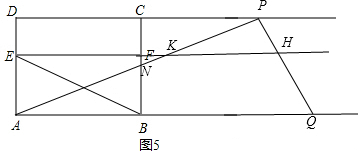
��APQ���ı���ABFE���ص����ֵ����S=S��ABN=$\frac{1}{2}$BN•AB=$\frac{1}{2}$��6����3$\sqrt{3}$-$\frac{3\sqrt{3}��t-6��}{t}$��=$\frac{54\sqrt{3}}{t}$��
����������APE���ı���ABFE���ص����ֵ����S=$\left\{\begin{array}{l}{\frac{4\sqrt{3}}{3}t+4\sqrt{3}��0��t��3��}\\{-\frac{\sqrt{3}}{2}{t}^{2}+\frac{13\sqrt{3}}{3}t-\frac{\sqrt{3}}{2}��3��t��5��}\\{-\frac{2\sqrt{3}}{3}t+12\sqrt{3}��5��t��9��}\\{\frac{54\sqrt{3}}{t}��t��9��}\end{array}\right.$��
���ڴ��ڵ�P��ʹ��BMNΪ���������Σ�
��3������ͼ6����MN=BN=3ʱ������DM��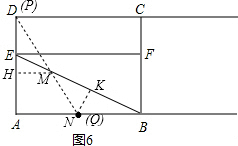
��AB=6��AD=3$\sqrt{3}$����E��AD�����ȷֵ㣬��AE��DE��AB���е�ΪN��
��AE=2$\sqrt{3}$��
���ABE=30�㣬
���ABE=��BMN=30��BE=4$\sqrt{3}$
��NK��BE����BE�ڵ�K��MH��AD��
��BN=3��
��MK=BK=$\frac{3\sqrt{3}}{2}$��
��EM=$\sqrt{3}$��
�ߡ�AEB�ס�HEM��
��$\frac{EM}{BE}$=$\frac{MH}{AN}$����$\frac{\sqrt{3}}{4\sqrt{3}}$=$\frac{MH}{6}$�����MH=$\frac{3}{2}$��
ͬ��EH=$\frac{\sqrt{3}}{2}$��
��DH=$\frac{3\sqrt{3}}{2}$��
���HDM=30�㣬
��DM��MN��һ��ֱ���ϣ���P����D���غϣ�Q����N���غϣ�
��t=0ʱ�����ڵ�P��ʹ��BMNΪ���������Σ�
����ͼ7����BM=BN=3ʱ������M��KH��CD����CD�ڵ�K��AB�ڵ�H��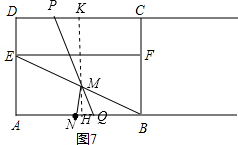
�ߡ�ABE=30�㣬
��MH=$\frac{3}{2}$��BH=$\frac{3\sqrt{3}}{2}$��
��KM=3$\sqrt{3}$-$\frac{3}{2}$��AH=6-$\frac{3\sqrt{3}}{2}$��
�ߡ�PQA=60�㣬
���MPK=60�㣬
��PK=$\frac{3\sqrt{3}-\frac{3}{2}}{\sqrt{3}}$=3-$\frac{3}{2}$��
��DP=AH-PK=DK-PK=6-$\frac{3\sqrt{3}}{2}$-��3-$\frac{\sqrt{3}}{2}$��=3-$\sqrt{3}$��
�൱t=3-$\sqrt{3}$ʱ�����ڵ�P��ʹ��BMNΪ���������Σ�
����ͼ8����MN=MBʱ������M��KH��CD����CD�ڵ�K��AB�ڵ�H��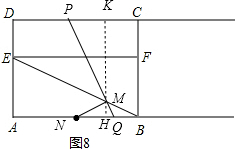
�ߡ�ABE=30�㣬
��MH=$\frac{\sqrt{3}}{2}$��BH=$\frac{3}{2}$��
��KM=3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$��AH=6-$\frac{3}{2}$=$\frac{9}{2}$��
�ߡ�PQA=60�㣬
���MPK=60�㣬
��PK=��3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$����$\sqrt{3}$=$\frac{5}{2}$��
��DP=AH-PK=DK-PK=$\frac{9}{2}$-$\frac{5}{2}$=2��
�൱t=2ʱ�����ڵ�P��ʹ��BMNΪ���������Σ�
����������t=0��t=3-$\sqrt{3}$��t=2ʱ�����ڵ�P��ʹ��BMNΪ���������Σ�
���� ������Ҫ�������ı����ۺ��⣬�漰���������ε����ʣ��������⣬ƽ���ı��ε����ʼ������Σ��ı��ε������ʽ������Ĺؼ�����ȷ�Ļ���ͼ�Σ���������ۣ��ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
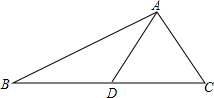 ��ͼ��ʾ���ڡ�ABC�У�AD��BC���ϵ����ߣ���AD=$\frac{1}{2}$BC��
��ͼ��ʾ���ڡ�ABC�У�AD��BC���ϵ����ߣ���AD=$\frac{1}{2}$BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ĸ��� | B�� | ��С�ķǸ��� | ||
| C�� | ���ĸ����� | D�� | ����ֵ��С�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������ABCD�У�AC=16��BD=12�������ε��ܳ��ǣ�������
��ͼ������ABCD�У�AC=16��BD=12�������ε��ܳ��ǣ�������| A�� | 20 | B�� | 24 | C�� | 28 | D�� | 40 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com