
【题目】已知:![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 延长线上的任意一点,过点
延长线上的任意一点,过点![]() 作
作![]() 的切线,切点为
的切线,切点为![]() ,
,![]() 的平分线
的平分线![]() 与
与![]() 交于点
交于点![]() .
.
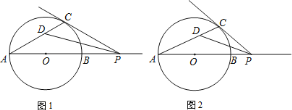
(1)如图![]() ,若
,若![]() 恰好等于
恰好等于![]() ,求
,求![]() 的度数;
的度数;
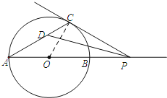
(2)如图![]() ,若点
,若点![]() 位于
位于![]() 中不同的位置,
中不同的位置,![]() 的结论是否仍然成立?说明你的理由.
的结论是否仍然成立?说明你的理由.
【答案】(1)![]() ;(2)
;(2)![]() 的大小不发生变化.理由见解析.
的大小不发生变化.理由见解析.
【解析】
(1)连接OC,则∠OCP=90°,根据∠CPA=30°,求得∠COP,再由OA=OC,得出∠A=∠ACO,由PD平分∠APC,即可得出∠CDP=45°.
(2)由PC是⊙O的切线,得∠OCP=90°.再根据PD是∠CPA的平分线,得∠APC=2∠APD.根据OA=OC,可得出∠A=∠ACO,即∠COP=2∠A,在Rt△OCP中,∠OCP=90°,则∠COP+∠OPC=90°,从而得出∠CDP=∠A+∠APD=45°.所以∠CDP的大小不发生变化.
![]() 连接
连接![]() ,
,
∵![]() 是
是![]() 的切线,
的切线,
∴![]()
∴![]() .
.
∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]()
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)![]() 的大小不发生变化.
的大小不发生变化.
∵![]() 是
是![]() 的切线,
的切线,
∴![]() .
.
∵![]() 是
是![]() 的平分线,
的平分线,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
即![]() 的大小不发生变化.
的大小不发生变化.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
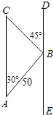
【题目】一架外国侦察机沿![]() 方向侵入我国领空进行非法侦察,我空军的战斗机沿
方向侵入我国领空进行非法侦察,我空军的战斗机沿![]() 方向与外国侦察机平行飞行,进行跟踪监视,我机在
方向与外国侦察机平行飞行,进行跟踪监视,我机在![]() 处与外国侦察机
处与外国侦察机![]() 处的距离为
处的距离为![]() 米,
米,![]() 为
为![]() ,这时外国侦察机突然转向,以偏左
,这时外国侦察机突然转向,以偏左![]() 的方向飞行,我机继续沿
的方向飞行,我机继续沿![]() 方向以
方向以![]() 米/秒的速度飞行,外国侦察机在
米/秒的速度飞行,外国侦察机在![]() 点故意撞击我战斗机,使我战斗机受损.问外国侦察机由
点故意撞击我战斗机,使我战斗机受损.问外国侦察机由![]() 到
到![]() 的速度是多少?(结果保留整数,参考数据
的速度是多少?(结果保留整数,参考数据![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC≌Rt△CED,点B、C、E在同一直线上,则结论:①AC=CD,②AC⊥CD,③BE=AB+DE,④AB∥ED,其中成立的有( )

A. 仅① B. 仅①③ C. 仅①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的平分线BF交DE于△ABC内一点P,连接PC.
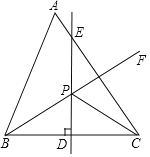
(1)若∠ABP=32°,求∠ACP的度数;
(2)若∠ACP=m°,∠ABP=n°,请直接写出m,n满足的关系式:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
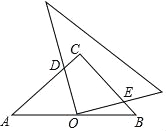
【题目】如图,在等腰Rt△ABC中,∠C=90°,点O是AB的中点,边AC的长为6,将一块边长足够长的三角板的直角顶点放在O点处,将三角板绕着点O旋转,始终保持三角板的直角边与AC相交,交点为点D,另一条直角边与BC相交,交点为点E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为( )
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与直线都经过坐标轴的正半轴上A(4,0),B两点,该抛物线的对称轴x=﹣1,与x轴交于点C,且∠ABC=90°,求:
(1)直线AB的解析式;
(2)抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.
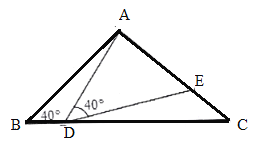
(1)当![]() 时,
时,![]() ______________
______________![]() ;点
;点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐变____________(填“大”或“小”);
逐渐变____________(填“大”或“小”);
(2)当![]() 时,求证:
时,求证:![]() ,请说明理由;
,请说明理由;
(3)在点![]() 的运动过程中,
的运动过程中,![]() 的形状也在改变,判断当
的形状也在改变,判断当![]() 等于多少度时,
等于多少度时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com